Вогнутая функция

Отрицательная выпуклая функция

В математике вогнутая функция — это функция, для которой значение функции в любой выпуклой комбинации элементов в области определения больше или равно этой выпуклой комбинации этих элементов области определения. Эквивалентно, вогнутая функция — это любая функция, для которой гипограф является выпуклым. Класс вогнутых функций в некотором смысле противоположен классу выпуклых функций . Вогнутая функция также синонимично называется вогнутой вниз , вогнутой вниз , выпуклой вверх , выпуклой крышкой или верхней выпуклой .

Определение

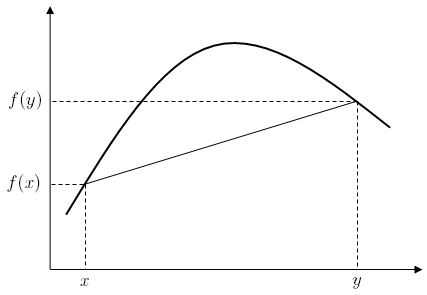
Действительная функция на интервале (или, в более общем смысле, выпуклое множество в векторном пространстве ) называется вогнутой , если для любых и в интервале и для любых , ^[1] $f$ $x$ $у$ $\альфа \in [0,1]$

f((1-\alpha)x+\alpha y)\geq (1-\alpha)f(x)+\alpha f(y)

Функция называется строго вогнутой, если дополнительно выполняются и . $\альфа \in (0,1)$ $x\neq y$

Для функции это второе определение просто утверждает, что для каждого значения строго между и точка на графике находится выше прямой линии, соединяющей точки и . $f:\mathbb {R} \to \mathbb {R}$ $z$ $x$ $у$ $(z,f(z))$ $f$ $(x,f(x))$ $(y,f(y))$

Функция является квазивогнутой , если верхние контурные множества функции являются выпуклыми множествами. ^[2] $f$ $S(a)=\{x:f(x)\geq a\}$

Характеристики

Функции одной переменной

Дифференцируемая функция f $является$ (строго) вогнутой на интервале тогда и только тогда, когда ее производная функция $f '$ является (строго) монотонно убывающей на этом интервале, то есть вогнутая функция имеет невозрастающий (убывающий) наклон . ^[3]^[4]
Точки , где вогнутость меняется (между вогнутостью и выпуклостью ), являются точками перегиба . ^[5]
Если $f$ дважды дифференцируема , то $f$ вогнута тогда и только тогда, когда $f ''$ неположительна (или, неформально, если « ускорение» неположительно). Если f ′′ отрицательна , то $f$ строго $вогнута$ , $но$ обратное неверно, как показывает $f$ ( $x$ $) = -$ $x$ $4$ .
Если $f$ вогнута и дифференцируема, то она ограничена сверху своим приближением Тейлора первого порядка : ^[2] $f(y)\leq f(x)+f'(x)[yx]$
Измеримая по Лебегу функция на интервале $C$ является вогнутой тогда и только тогда, когда она является вогнутой в средней точке, то есть для любых $x$ и $y$ в $C$ $f\left({\frac {x+y}{2}}\right)\geq {\frac {f(x)+f(y)}{2}}$
Если функция f вогнута и f (0) ≥ 0 , то f субаддитивна на . Доказательство: $[0,\infty )$
- Так как $f$ вогнута и $1 \geq t \geq 0$ , то, положив $y = 0,$ мы имеем $f(tx)=f(tx+(1-t)\cdot 0)\geq tf(x)+(1-t)f(0)\geq tf(x).$
- Для : $a,b\in [0,\infty )$ $f(a)+f(b)=f\left((a+b){\frac {a}{a+b}}\right)+f\left((a+b){\frac {b}{a+b}}\right)\geq {\frac {a}{a+b}}f(a+b)+{\frac {b}{a+b}}f(a+b)=f(a+b)$

Функциинпеременные

Функция $f$ является вогнутой над выпуклым множеством тогда и только тогда, когда функция $-f$ является выпуклой функцией над этим множеством.
Сумма двух вогнутых функций сама по себе вогнута, как и поточечный минимум двух вогнутых функций, т.е. множество вогнутых функций на данной области образует полуполе .
Вблизи строгого локального максимума внутри области определения функции функция должна быть вогнутой; как частичное обратное утверждение, если производная строго вогнутой функции равна нулю в некоторой точке, то эта точка является локальным максимумом.
Любой локальный максимум вогнутой функции также является глобальным максимумом . Строго вогнутая функция будет иметь не более одного глобального максимума.

Примеры

Функции и вогнуты на своих областях определения, так как их вторые производные и всегда отрицательны. $f(x)=-x^{2}$ $g(x)={\sqrt {x}}$ $f''(x)=-2$ ${\textstyle g''(x)=-{\frac {1}{4x^{3/2}}}}$
Функция логарифма является вогнутой на своей области определения , поскольку ее производная является строго убывающей функцией. $f(x)=\log {x}$ $(0,\infty)$ ${\frac {1}{x}}$
Любая аффинная функция является как вогнутой, так и выпуклой, но не является ни строго вогнутой, ни строго выпуклой. $f(x)=ax+b$
Функция синуса вогнута на интервале . $[0,\пи]$
Функция , где — определитель неотрицательно -определенной матрицы B , является вогнутой. ^[6] $f(B)=\log |B|$ $|Б|$

Приложения

Искривление лучей при расчете затухания радиоволн в атмосфере подразумевает вогнутые функции.
В теории ожидаемой полезности для выбора в условиях неопределенности кардинальные функции полезности лиц , принимающих решения , не склонных к риску, являются вогнутыми.
В микроэкономической теории производственные функции обычно предполагаются вогнутыми в некоторых или во всех своих областях, что приводит к убывающей отдаче от факторов производства. ^[7]
В термодинамике и теории информации энтропия является вогнутой функцией. В случае термодинамической энтропии без фазового перехода энтропия как функция экстенсивных переменных является строго вогнутой. Если система может претерпеть фазовый переход и если ей разрешено разделиться на две подсистемы с различной фазой ( разделение фаз , например, кипение), максимальные по энтропии параметры подсистем приведут к объединенной энтропии точно на прямой линии между двумя фазами. Это означает, что «эффективная энтропия» системы с фазовым переходом является выпуклой оболочкой энтропии без разделения фаз; следовательно, энтропия системы, включающей разделение фаз, будет нестрого вогнутой. ^[8]

Смотрите также

Ссылки

^ Ленхарт, С.; Воркман, Дж. Т. (2007). Оптимальное управление, применяемое к биологическим моделям . Серия «Математическая и вычислительная биология». Chapman & Hall/CRC. ISBN 978-1-58488-640-2.
^ ab Varian, Hal R. (1992). Микроэкономический анализ (3-е изд.). Нью-Йорк: Norton. стр. 489. ISBN 0-393-95735-7. OCLC 24847759.
^ Рудин, Уолтер (1976). Анализ . стр. 101.
^ Градштейн, И.С.; Рыжик, И.М.; Хейс, Д.Ф. (1976-07-01). "Таблица интегралов, рядов и произведений". Журнал технологии смазки . 98 (3): 479. doi : 10.1115/1.3452897 . ISSN 0022-2305.
^ Хасс, Джоэл (13 марта 2017 г.). Исчисление Томаса. Хейл, Кристофер, 1960-, Вейр, Морис Д., Томас, Джордж Б. младший (Джордж Бринтон), 1914-2006. (Четырнадцатое изд.). [Соединенные Штаты]. стр. 203. ISBN 978-0-13-443898-6. OCLC 965446428.{{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )
^ Кавер, Томас М.; Томас, JA (1988). «Определяющие неравенства через теорию информации». Журнал SIAM по матричному анализу и приложениям . 9 (3): 384–392 . doi :10.1137/0609033. S2CID 5491763.
^ Пембертон, Малкольм; Рау, Николас (2015). Математика для экономистов: вводный учебник. Oxford University Press. С. 363–364 . ISBN 978-1-78499-148-7.
^ Каллен, Герберт Б.; Каллен, Герберт Б. (1985). "8.1: Внутренняя устойчивость термодинамических систем". Термодинамика и введение в термостатику (2-е изд.). Нью-Йорк: Wiley. С. 203–206 . ISBN 978-0-471-86256-7.

Дополнительные ссылки

Крузе, Ж.-П. (2008). «Квазивогнутость». В Дурлауф, Стивен Н.; Блюм, Лоуренс Э. (ред.). Новый экономический словарь Пэлгрейва (второе изд.). Palgrave Macmillan. стр. 815– 816. doi :10.1057/9780230226203.1375. ISBN 978-0-333-78676-5.
Рао, Сингиресу С. (2009). Инженерная оптимизация: теория и практика . John Wiley and Sons. стр. 779. ISBN 978-0-470-18352-6.

[1] Ленхарт, С.; Воркман, Дж. Т. (2007). Оптимальное управление, применяемое к биологическим моделям . Серия «Математическая и вычислительная биология». Chapman & Hall/CRC. ISBN 978-1-58488-640-2.

[:0-2] Varian, Hal R. (1992). Микроэкономический анализ (3-е изд.). Нью-Йорк: Norton. стр. 489. ISBN 0-393-95735-7. OCLC 24847759.

[3] Рудин, Уолтер (1976). Анализ . стр. 101.

[4] Градштейн, И.С.; Рыжик, И.М.; Хейс, Д.Ф. (1976-07-01). "Таблица интегралов, рядов и произведений". Журнал технологии смазки . 98 (3): 479. doi : 10.1115/1.3452897 . ISSN 0022-2305.

[5] Хасс, Джоэл (13 марта 2017 г.). Исчисление Томаса. Хейл, Кристофер, 1960-, Вейр, Морис Д., Томас, Джордж Б. младший (Джордж Бринтон), 1914-2006. (Четырнадцатое изд.). [Соединенные Штаты]. стр. 203. ISBN 978-0-13-443898-6. OCLC 965446428.{{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )

[Cover_1988-6] Кавер, Томас М.; Томас, JA (1988). «Определяющие неравенства через теорию информации». Журнал SIAM по матричному анализу и приложениям . 9 (3): 384–392 . doi :10.1137/0609033. S2CID 5491763.

[7] Пембертон, Малкольм; Рау, Николас (2015). Математика для экономистов: вводный учебник. Oxford University Press. С. 363–364 . ISBN 978-1-78499-148-7.

[8] Каллен, Герберт Б.; Каллен, Герберт Б. (1985). "8.1: Внутренняя устойчивость термодинамических систем". Термодинамика и введение в термостатику (2-е изд.). Нью-Йорк: Wiley. С. 203–206 . ISBN 978-0-471-86256-7.