Напряжение (механика)
This article needs additional citations for verification. (August 2021) |
| Стресс | |
|---|---|
 Остаточные напряжения внутри пластикового транспортира выявляются с помощью поляризованного света . | |
Общие символы | σ |
| единица СИ | паскаль |
Другие единицы | фунт/кв . дюйм , бар |
| В основных единицах СИ | Па = кг ⋅ м −1 ⋅ с −2 |
| Измерение | |
| Part of a series on |
| Continuum mechanics |
|---|
В механике сплошной среды напряжение — это физическая величина , которая описывает силы, присутствующие во время деформации . Например, объект, который растягивается, например, растянутая эластичная лента, подвергается растягивающему напряжению и может удлиняться . Объект, который сжимается, например, смятая губка, подвергается сжимающему напряжению и может укорачиваться. [1] [2] Чем больше сила и чем меньше площадь поперечного сечения тела, на которое она действует, тем больше напряжение. Напряжение имеет размерность силы на площадь, с единицами СИ ньютонами на квадратный метр (Н/м 2 ) или паскалем (Па). [1]
Напряжение выражает внутренние силы, которые соседние частицы сплошного материала оказывают друг на друга, в то время как деформация является мерой относительной деформации материала. [3] Например, когда сплошной вертикальный стержень поддерживает верхний вес , каждая частица в стержне толкает частицы, находящиеся непосредственно под ним. Когда жидкость находится в закрытом контейнере под давлением , каждая частица толкается всеми окружающими частицами. Стенки контейнера и поверхность, вызывающая давление (например, поршень), толкают их в (ньютоновской) реакции . Эти макроскопические силы на самом деле являются чистым результатом очень большого числа межмолекулярных сил и столкновений между частицами в этих молекулах . Напряжение часто обозначается строчной греческой буквой сигма ( σ ). [3]
Напряжение внутри материала может возникать под действием различных механизмов, таких как напряжение , приложенное внешними силами к объемному материалу (например, сила тяжести ) или к его поверхности (например, контактные силы , внешнее давление или трение ). Любое напряжение (деформация) твердого материала создает внутреннее упругое напряжение , аналогичное силе реакции пружины , которая стремится вернуть материал в его первоначальное недеформированное состояние. В жидкостях и газах только деформации, которые изменяют объем, создают постоянное упругое напряжение. Если деформация постепенно изменяется со временем, даже в жидкостях обычно будет некоторое вязкое напряжение , противодействующее этому изменению. Упругие и вязкие напряжения обычно объединяют под названием механическое напряжение .

Значительное напряжение может существовать даже тогда, когда деформация незначительна или отсутствует (обычное предположение при моделировании потока воды). Напряжение может существовать и при отсутствии внешних сил; такое встроенное напряжение важно, например, в предварительно напряженном бетоне и закаленном стекле . Напряжение также может быть наложено на материал без приложения чистых сил , например, за счет изменений температуры или химического состава, или внешних электромагнитных полей (как в пьезоэлектрических и магнитострикционных материалах).
Связь между механическим напряжением, деформацией и скоростью деформации может быть довольно сложной, хотя линейное приближение может быть адекватным на практике, если величины достаточно малы. Напряжение, превышающее определенные пределы прочности материала, приведет к постоянной деформации (такой как пластическое течение , трещина , кавитация ) или даже изменит его кристаллическую структуру и химический состав .
История
Люди знали о напряжении внутри материалов с древних времен. До 17 века это понимание было в значительной степени интуитивным и эмпирическим, хотя это не помешало развитию относительно передовых технологий, таких как композитный лук и выдувание стекла . [4]
На протяжении нескольких тысячелетий архитекторы и строители, в частности, учились соединять тщательно сформированные деревянные балки и каменные блоки, чтобы выдерживать, передавать и распределять нагрузку наиболее эффективным образом, с помощью таких изобретательных устройств, как капители , арки , купола , фермы и аркбутаны готических соборов .
Древние и средневековые архитекторы разработали некоторые геометрические методы и простые формулы для вычисления надлежащих размеров столбов и балок, но научное понимание напряжения стало возможным только после изобретения необходимых инструментов в 17-м и 18-м веках: строгий экспериментальный метод Галилео Галилея , координаты и аналитическая геометрия Рене Декарта , а также законы движения и равновесия Ньютона и исчисление бесконечно малых . [5] С помощью этих инструментов Огюстен-Луи Коши смог дать первую строгую и общую математическую модель деформированного упругого тела, введя понятия напряжения и деформации. [6] Коши заметил, что сила на воображаемой поверхности является линейной функцией ее нормального вектора; и, более того, что она должна быть симметричной функцией (с нулевым общим импульсом). Понимание напряжения в жидкостях началось с Ньютона, который предоставил дифференциальную формулу для сил трения (напряжения сдвига) в параллельном ламинарном потоке .
Определение
Напряжение определяется как сила, действующая на небольшую границу на единицу площади этой границы для всех ориентаций границы. [7] Выведенное из фундаментальной физической величины (силы) и чисто геометрической величины (площади), напряжение также является фундаментальной величиной, как скорость, крутящий момент или энергия , которая может быть количественно определена и проанализирована без явного рассмотрения природы материала или его физических причин.

Следуя основным предпосылкам механики сплошной среды, напряжение является макроскопическим понятием. А именно, частицы, рассматриваемые в его определении и анализе, должны быть достаточно малы, чтобы их можно было считать однородными по составу и состоянию, но все же достаточно велики, чтобы игнорировать квантовые эффекты и детальные движения молекул. Таким образом, сила между двумя частицами на самом деле является средним значением очень большого числа атомных сил между их молекулами; и физические величины, такие как масса, скорость и силы, которые действуют через объем трехмерных тел, такие как гравитация, предполагаются плавно распределенными по ним. [8] : 90–106 В зависимости от контекста можно также предположить, что частицы достаточно велики, чтобы допустить усреднение других микроскопических характеристик, таких как зерна металлического стержня или волокна куска дерева .
Количественно напряжение выражается вектором тяги Коши T, определяемым как сила тяги F между соседними частями материала через воображаемую разделяющую поверхность S , деленная на площадь S. [9] : 41–50 В покоящейся жидкости сила перпендикулярна поверхности и является известным давлением . В твердом теле или в потоке вязкой жидкости сила F может не быть перпендикулярна S ; следовательно, напряжение на поверхности следует рассматривать как векторную величину, а не скаляр. Более того, направление и величина обычно зависят от ориентации S . Таким образом, напряженное состояние материала должно описываться тензором , называемым тензором напряжений (Коши) ; который является линейной функцией , связывающей нормальный вектор n поверхности S с вектором тяги T через S . Относительно любой выбранной системы координат тензор напряжений Коши можно представить в виде симметричной матрицы 3×3 действительных чисел. Даже внутри однородного тела тензор напряжений может меняться от места к месту и со временем; поэтому напряжение внутри материала, в общем случае, представляет собой изменяющееся во времени тензорное поле .
Нормальный и сдвигающий
В общем случае напряжение T , которое частица P прикладывает к другой частице Q через поверхность S, может иметь любое направление относительно S. Вектор T можно рассматривать как сумму двух компонентов: нормального напряжения ( сжатия или растяжения ), перпендикулярного поверхности, и касательного напряжения , параллельного поверхности.
Если нормальный единичный вектор n поверхности (направленный от Q к P ) предполагается фиксированным, то нормальный компонент может быть выражен одним числом, скалярным произведением T · n . Это число будет положительным, если P «тянет» Q (напряжение растяжения), и отрицательным, если P «толкает» Q (напряжение сжатия). Тогда компонент сдвига равен вектору T − ( T · n ) n .
Единицы
Размерность напряжения равна размерности давления , и поэтому его координаты измеряются в тех же единицах, что и давление: а именно, паскалях (Па, то есть ньютонах на квадратный метр ) в Международной системе или фунтах на квадратный дюйм (psi) в Имперской системе . Поскольку механические напряжения легко превышают миллион Паскалей, МПа, что означает мегапаскаль, является общепринятой единицей измерения напряжения.
Причины и следствия

Напряжение в материальном теле может быть вызвано несколькими физическими причинами, включая внешние воздействия и внутренние физические процессы. Некоторые из этих агентов (такие как гравитация, изменения температуры и фазы , а также электромагнитные поля) действуют на большую часть материала, непрерывно изменяясь в зависимости от положения и времени. Другие агенты (такие как внешние нагрузки и трение, давление окружающей среды и контактные силы) могут создавать напряжения и силы, которые концентрируются на определенных поверхностях, линиях или точках; и, возможно, также на очень коротких временных интервалах (как в импульсах из -за столкновений). В активной материи самодвижение микроскопических частиц генерирует макроскопические профили напряжений. [11] В общем случае распределение напряжений в теле выражается как кусочно- непрерывная функция пространства и времени.
Наоборот, напряжение обычно коррелирует с различными эффектами на материал, возможно, включая изменения физических свойств, таких как двулучепреломление , поляризация и проницаемость . Наложение напряжения внешним агентом обычно создает некоторую деформацию (напряжение) в материале, даже если она слишком мала, чтобы ее можно было обнаружить. В твердом материале такая деформация, в свою очередь, создает внутреннее упругое напряжение, аналогичное силе реакции растянутой пружины , стремящейся восстановить материал в его первоначальном недеформированном состоянии. Жидкие материалы (жидкости, газы и плазма ) по определению могут противостоять только деформациям, которые изменят их объем. Если деформация изменяется со временем, даже в жидкостях обычно будет некоторое вязкое напряжение, противодействующее этому изменению. Такие напряжения могут быть как сдвиговыми, так и нормальными по своей природе. Молекулярное происхождение сдвиговых напряжений в жидкостях приведено в статье о вязкости . То же самое для нормальных вязких напряжений можно найти в Sharma (2019). [12]
Связь между напряжением и его эффектами и причинами, включая деформацию и скорость изменения деформации, может быть довольно сложной (хотя линейное приближение может быть адекватным на практике, если величины достаточно малы). Напряжение, превышающее определенные пределы прочности материала, приведет к постоянной деформации (такой как пластическое течение , трещина , кавитация ) или даже изменит его кристаллическую структуру и химический состав .
Простые типы
В некоторых ситуациях напряжение внутри тела может быть адекватно описано одним числом или одним вектором (числом и направлением). Три таких простых напряженных ситуации, которые часто встречаются в инженерном проектировании, это одноосное нормальное напряжение , простое касательное напряжение и изотропное нормальное напряжение . [13]
Одноосный нормальный

Распространенной ситуацией с простой картиной напряжений является ситуация, когда прямой стержень с однородным материалом и поперечным сечением подвергается растяжению противоположными силами величины вдоль своей оси. Если система находится в равновесии и не меняется со временем, а весом стержня можно пренебречь, то через каждое поперечное сечение стержня верхняя часть должна тянуть нижнюю часть с той же силой, F с непрерывностью через всю площадь поперечного сечения , A . Следовательно, напряжение σ по всему стержню, по любой горизонтальной поверхности, может быть выражено просто одним числом σ, вычисленным просто с величиной этих сил, F , и площадью поперечного сечения, A . С другой стороны, если представить, что стержень разрезается по его длине, параллельно оси, не будет никакой силы (следовательно, никакого напряжения) между двумя половинами поперек разреза. Этот тип напряжения можно назвать (простым) нормальным напряжением или одноосным напряжением; в частности, (одноосным, простым и т. д.) растягивающим напряжением. [13] Если нагрузка на стержень сжимает его, а не растягивает, анализ тот же самый, за исключением того, что сила F и напряжение меняют знак, а напряжение называется сжимающим напряжением.

Этот анализ предполагает, что напряжение равномерно распределено по всему поперечному сечению. На практике, в зависимости от того, как стержень прикреплен на концах и как он был изготовлен, это предположение может быть неверным. В этом случае значение = F / A будет только средним напряжением, называемым инженерным напряжением или номинальным напряжением . Если длина стержня L во много раз больше его диаметра D и он не имеет грубых дефектов или встроенного напряжения, то можно предположить, что напряжение равномерно распределено по любому поперечному сечению, которое больше, чем несколько раз D с обоих концов. (Это наблюдение известно как принцип Сен-Венана ).
Нормальное напряжение возникает во многих других ситуациях, помимо осевого растяжения и сжатия. Если упругий стержень с равномерным и симметричным поперечным сечением изгибается в одной из его плоскостей симметрии, результирующее изгибающее напряжение все равно будет нормальным (перпендикулярным поперечному сечению), но будет изменяться по поперечному сечению: внешняя часть будет находиться под растягивающим напряжением, а внутренняя часть будет сжата. Другим вариантом нормального напряжения является кольцевое напряжение , которое возникает на стенках цилиндрической трубы или сосуда, заполненного жидкостью под давлением.
Сдвиг

Другой простой тип напряжения возникает, когда равномерно толстый слой эластичного материала, такого как клей или резина, прочно прикреплен к двум жестким телам, которые тянутся в противоположных направлениях силами, параллельными слою; или к секции мягкого металлического стержня, который разрезается губками инструмента, похожего на ножницы . Пусть F будет величиной этих сил, а M будет средней плоскостью этого слоя. Так же, как и в случае нормального напряжения, часть слоя по одну сторону от M должна тянуть другую часть с той же силой F . Предполагая, что направление сил известно, напряжение через M можно выразить просто одним числом , вычисленным просто с помощью величины этих сил, F и площади поперечного сечения, A . В отличие от нормального напряжения, это простое касательное напряжение направлено параллельно рассматриваемому поперечному сечению, а не перпендикулярно ему. [13] Для любой плоскости S , которая перпендикулярна слою, чистая внутренняя сила через S , а следовательно, и напряжение, будут равны нулю.
Как и в случае стержня, нагруженного по оси, на практике касательное напряжение может быть распределено неравномерно по слою; поэтому, как и прежде, отношение F / A будет только средним («номинальным», «инженерным») напряжением. Этого среднего значения часто бывает достаточно для практических целей. [14] : 292 Касательное напряжение наблюдается также, когда цилиндрический стержень, такой как вал, подвергается воздействию противоположных крутящих моментов на своих концах. В этом случае касательное напряжение на каждом поперечном сечении параллельно поперечному сечению, но ориентировано тангенциально относительно оси и увеличивается с расстоянием от оси. Значительное касательное напряжение возникает в средней пластине («стенке») двутавровых балок под изгибающими нагрузками из-за того, что стенка ограничивает торцевые пластины («фланцы»).
Изотропный
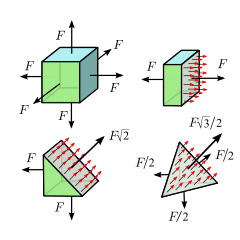
Другой простой тип напряжения возникает, когда материальное тело находится под одинаковым сжатием или растяжением во всех направлениях. Это имеет место, например, в части жидкости или газа в состоянии покоя, заключенной в какой-либо контейнер или как часть большей массы жидкости; или внутри куба из эластичного материала, который сжимается или тянется на всех шести гранях равными перпендикулярными силами — при условии, что в обоих случаях материал однороден, без встроенного напряжения, и что можно пренебречь влиянием гравитации и других внешних сил.
В этих ситуациях напряжение на любой воображаемой внутренней поверхности оказывается одинаковым по величине и всегда направлено перпендикулярно поверхности независимо от ориентации поверхности. Этот тип напряжения можно назвать изотропным нормальным или просто изотропным ; если оно сжимающее, оно называется гидростатическим давлением или просто давлением . Газы по определению не могут выдерживать растягивающие напряжения, но некоторые жидкости могут выдерживать очень большие количества изотропных растягивающих напряжений при некоторых обстоятельствах. см. Z-трубка .
Цилиндр
Детали с вращательной симметрией , такие как колеса, оси, трубы и столбы, очень распространены в машиностроении. Часто картины напряжений, возникающие в таких деталях, имеют вращательную или даже цилиндрическую симметрию . Анализ таких цилиндрических напряжений может использовать симметрию для уменьшения размерности домена и/или тензора напряжений.
Общие типы
Часто механические тела испытывают более одного типа напряжения одновременно; это называется комбинированным напряжением . При нормальном и касательном напряжении величина напряжения максимальна для поверхностей, перпендикулярных определенному направлению , и равна нулю на любых поверхностях, параллельных . Когда касательное напряжение равно нулю только на поверхностях, перпендикулярных одному конкретному направлению, напряжение называется двуосным и может рассматриваться как сумма двух нормальных или касательных напряжений. В самом общем случае, называемом трехосным напряжением , напряжение не равно нулю на каждом элементе поверхности.
Тензор Коши


Комбинированные напряжения не могут быть описаны одним вектором. Даже если материал нагружен одинаково по всему объему тела, напряжение на любой воображаемой поверхности будет зависеть от ориентации этой поверхности нетривиальным образом.
Коши заметил, что вектор напряжения на поверхности всегда будет линейной функцией вектора нормали поверхности , вектора единичной длины, который перпендикулярен ей. То есть, , где функция удовлетворяет для любых векторов и любых действительных чисел . Функция , теперь называемая тензором напряжений (Коши) , полностью описывает напряженное состояние равномерно напряженного тела. (Сегодня любая линейная связь между двумя физическими векторными величинами называется тензором , отражая первоначальное использование Коши для описания «напряжений» (напряжений) в материале.) В тензорном исчислении классифицируется как тензор второго порядка типа (0,2) или (1,1) в зависимости от соглашения.
Как и любое линейное отображение между векторами, тензор напряжений может быть представлен в любой выбранной декартовой системе координат матрицей 3×3 действительных чисел. В зависимости от того, пронумерованы ли координаты или названы , матрица может быть записана как или Вектор напряжений на поверхности с нормальным вектором (который является ковариантным - "строка; горизонтальный" - вектор) с координатами тогда является матричным произведением (где T в верхнем индексе - транспонирование , и в результате мы получаем ковариантный (строка) вектор) (см. тензор напряжений Коши ), то есть
Линейная связь между и следует из фундаментальных законов сохранения линейного импульса и статического равновесия сил, и поэтому является математически точной для любого материала и любой напряженной ситуации. Компоненты тензора напряжений Коши в каждой точке материала удовлетворяют уравнениям равновесия ( уравнения движения Коши для нулевого ускорения). Более того, принцип сохранения углового момента подразумевает, что тензор напряжений симметричен , то есть , , и . Поэтому напряженное состояние среды в любой точке и момент времени может быть задано только шестью независимыми параметрами, а не девятью. Их можно записать , где элементы называются ортогональными нормальными напряжениями (относительно выбранной системы координат) и ортогональными касательными напряжениями . [ необходима цитата ]
Изменение координат
Тензор напряжений Коши подчиняется закону преобразования тензора при изменении системы координат. Графическим изображением этого закона преобразования является круг распределения напряжений Мора .
Как симметричная вещественная матрица 3×3, тензор напряжений имеет три взаимно ортогональных собственных вектора единичной длины и три вещественных собственных значения , таких что . Следовательно, в системе координат с осями тензор напряжений является диагональной матрицей и имеет только три нормальных компонента λ 1 , λ 2 , λ 3 {\displaystyle \lambda _{1},\lambda _{2},\lambda _{3}} главные напряжения . Если три собственных значения равны, напряжение является изотропным сжатием или растяжением, всегда перпендикулярным любой поверхности, касательное напряжение отсутствует, и тензор является диагональной матрицей в любой системе координат.
Тензорное поле
В общем случае напряжение неравномерно распределено по материальному телу и может меняться со временем. Поэтому тензор напряжения должен быть определен для каждой точки и каждого момента, рассматривая бесконечно малую частицу среды, окружающую эту точку, и принимая средние напряжения в этой частице за напряжения в этой точке.
Тонкие пластины

Искусственно созданные объекты часто изготавливаются из пластин различных материалов с помощью операций, которые не меняют их по сути двумерный характер, таких как резка, сверление, плавный изгиб и сварка по краям. Описание напряжения в таких телах можно упростить, моделируя эти части как двумерные поверхности, а не как трехмерные тела.
В этом представлении «частица» переопределяется как бесконечно малый участок поверхности пластины, так что граница между соседними частицами становится бесконечно малым линейным элементом; оба неявно расширены в третьем измерении, перпендикулярно (прямо через) пластину. «Напряжение» затем переопределяется как мера внутренних сил между двумя соседними «частицами» через их общий линейный элемент, деленная на длину этой линии. Некоторые компоненты тензора напряжений можно игнорировать, но поскольку частицы не являются бесконечно малыми в третьем измерении, больше нельзя игнорировать крутящий момент, который частица прикладывает к своим соседям. Этот крутящий момент моделируется как изгибающее напряжение , которое имеет тенденцию изменять кривизну пластины. Эти упрощения могут не работать на сварных швах, на резких изгибах и складках (где радиус кривизны сопоставим с толщиной пластины).
Тонкие балки

Анализ напряжения может быть значительно упрощен также для тонких стержней, балок или проводов однородного (или плавно изменяющегося) состава и поперечного сечения, которые подвергаются умеренному изгибу и скручиванию. Для таких тел можно рассматривать только поперечные сечения, перпендикулярные оси стержня, и переопределять «частицу» как кусок проволоки с бесконечно малой длиной между двумя такими поперечными сечениями. Обычное напряжение тогда сводится к скаляру (растяжение или сжатие стержня), но необходимо также учитывать изгибающее напряжение (которое пытается изменить кривизну стержня в некотором направлении, перпендикулярном оси) и крутильное напряжение (которое пытается скрутить или раскрутить его вокруг своей оси).
Анализ
Анализ напряжений — это раздел прикладной физики , который охватывает определение внутреннего распределения внутренних сил в твердых объектах. Это важный инструмент в инженерии для изучения и проектирования таких конструкций, как туннели, плотины, механические детали и структурные каркасы, под заданными или ожидаемыми нагрузками. Он также важен во многих других дисциплинах; например, в геологии для изучения таких явлений, как тектоника плит , вулканизм и лавины ; и в биологии для понимания анатомии живых существ.
Цели и предположения
Анализ напряжений обычно касается объектов и структур, которые можно считать находящимися в макроскопическом статическом равновесии . Согласно законам движения Ньютона , любые внешние силы, приложенные к такой системе, должны быть уравновешены внутренними силами реакции, [15] : 97 которые почти всегда являются силами поверхностного контакта между соседними частицами — то есть, как напряжение. [9] Поскольку каждая частица должна находиться в равновесии, это напряжение реакции, как правило, будет распространяться от частицы к частице, создавая распределение напряжения по всему телу. Типичная проблема в анализе напряжений состоит в определении этих внутренних напряжений с учетом внешних сил, действующих на систему. Последние могут быть силами тела (такими как сила тяжести или магнитное притяжение), которые действуют по всему объему материала; [16] : 42–81 или сосредоточенными нагрузками (такими как трение между осью и подшипником или вес колеса поезда на рельсе), которые, как предполагается, действуют в двумерной области, или вдоль линии, или в одной точке.
При анализе напряжений обычно игнорируют физические причины сил или точную природу материалов. Вместо этого предполагается, что напряжения связаны с деформацией (и, в нестатических задачах, со скоростью деформации) материала известными конститутивными уравнениями . [17]
Методы
Анализ напряжений может быть выполнен экспериментально, путем приложения нагрузок к реальному артефакту или к масштабной модели и измерения полученных напряжений любым из нескольких доступных методов. Этот подход часто используется для сертификации и мониторинга безопасности. Большая часть напряжений анализируется математическими методами, особенно во время проектирования. Основная задача анализа напряжений может быть сформулирована с помощью уравнений движения Эйлера для непрерывных тел (которые являются следствиями законов Ньютона для сохранения линейного импульса и момента импульса ) и принципа напряжений Эйлера-Коши вместе с соответствующими конститутивными уравнениями. Таким образом, получается система уравнений в частных производных, включающая поле тензора напряжений и поле тензора деформаций в качестве неизвестных функций, которые необходимо определить. Внешние силы тела появляются как независимый («правая часть») член в дифференциальных уравнениях, в то время как сосредоточенные силы появляются как граничные условия. Таким образом, основная задача анализа напряжений является краевой задачей .
Анализ напряжений для упругих конструкций основан на теории упругости и теории бесконечно малых деформаций . Когда приложенные нагрузки вызывают постоянную деформацию, необходимо использовать более сложные уравнения состояния, которые могут учитывать вовлеченные физические процессы ( пластическое течение , разрушение , фазовый переход и т. д.). Инженерные конструкции обычно проектируются так, чтобы максимальные ожидаемые напряжения находились в пределах линейной упругости (обобщение закона Гука для сплошных сред); то есть деформации, вызванные внутренними напряжениями, линейно связаны с ними. В этом случае дифференциальные уравнения, определяющие тензор напряжений, являются линейными, и задача становится намного проще. Во-первых, напряжение в любой точке также будет линейной функцией нагрузок. Для достаточно малых напряжений даже нелинейные системы обычно можно считать линейными.

Анализ напряжений упрощается, когда физические размеры и распределение нагрузок позволяют рассматривать конструкцию как одномерную или двумерную. Например, при анализе ферм поле напряжений можно считать однородным и одноосным по каждому элементу. Тогда дифференциальные уравнения сводятся к конечному набору уравнений (обычно линейных) с конечным числом неизвестных. В других контекстах можно свести трехмерную задачу к двумерной и/или заменить общие тензоры напряжений и деформаций более простыми моделями, такими как одноосное растяжение/сжатие, простой сдвиг и т. д.
Тем не менее, для двух- или трехмерных случаев необходимо решить задачу уравнения в частных производных. Аналитические или замкнутые решения дифференциальных уравнений могут быть получены, когда геометрия, определяющие соотношения и граничные условия достаточно просты. В противном случае обычно приходится прибегать к численным приближениям, таким как метод конечных элементов , метод конечных разностей и метод граничных элементов .
Меры
Другие полезные меры напряжения включают первый и второй тензоры напряжений Пиолы–Кирхгофа , тензор напряжений Био и тензор напряжений Кирхгофа .
Смотрите также
| Conjugate variables of thermodynamics | ||||||||
|
- Изгиб
- Прочность на сжатие
- Анализ критической плоскости
- Микроскоп с зондом Кельвина
- Круг Мора
- Эллипсоид напряжений Ламе
- Усиленный сплошной
- Остаточное напряжение
- Прочность на сдвиг
- Дробеструйная обработка
- Напряжение
- Тензор деформации
- Тензор скорости деформации
- Тензор энергии-напряжения
- Кривая напряжение-деформация
- Концентрация напряжения
- Кратковременная нагрузка трения
- Предел прочности
- Термический стресс
- Вирусный стресс
- Выход (инжиниринг)
- Поверхность текучести
- Теорема вириала
Ссылки
- ^ ab "12.3 Напряжение, деформация и модуль упругости - Университетская физика, том 1 | OpenStax". openstax.org . 19 сентября 2016 г. Получено 2022-11-02 .
- ^ "Класс Физическая-Величина в теории Физических-Величин". www-ksl.stanford.edu . Получено 2022-11-02 .
- ^ ab "Что такое напряжение сдвига - Материалы - Определение". Свойства материалов . 2020-07-31 . Получено 2022-11-02 .
- ^ Гордон, Дж. Э. (2003). Структуры, или Почему вещи не падают (2. Da Capo Press ed.). Кембридж, Массачусетс: Da Capo Press. ISBN 0306812835.
- ^ Якоб Люблинер (2008). "Теория пластичности" Архивировано 31.03.2010 в Wayback Machine (пересмотренное издание). Dover Publications. ISBN 0-486-46290-0
- ^ https://archive.org/details/historyofstrengt0000timo_k8r2/page/110/mode/2up, стр.107-110
- ^ Вай-Фа Чен и Да-Джиан Хан (2007), «Пластичность для инженеров-строителей». J. Ross Publishing ISBN 1-932159-75-4
- ^ Питер Чедвик (1999), «Механика сплошной среды: краткая теория и проблемы». Dover Publications, серия «Книги по физике». ISBN 0-486-40180-4 . страницы
- ^ ab I-Shih Liu (2002), "Механика сплошной среды". Springer ISBN 3-540-43019-9
- ^ (2009) Искусство изготовления стекла. Брошюра продукции Lamberts Glashütte (LambertsGlas). Доступ 08.02.2013.
- ^ Marchetti, MC; Joanny, JF; Ramaswamy, S.; Liverpool, TB; Prost, J.; Rao, Madan; Simha, R. Aditi (2013). «Гидродинамика мягкой активной материи». Reviews of Modern Physics . 85 (3): 1143–1189. Bibcode : 2013RvMP...85.1143M. doi : 10.1103/RevModPhys.85.1143.
- ^ Шарма, Б. и Кумар, Р. «Оценка объемной вязкости разбавленных газов с использованием подхода неравновесной молекулярной динамики». Physical Review E , 100, 013309 (2019)
- ^ abc Рональд Л. Хьюстон и Гарольд Джозефс (2009), «Практический анализ напряжений в инженерном проектировании». 3-е издание, CRC Press, 634 страницы. ISBN 9781574447132
- ^ Уолтер Д. Пилки, Оррин Х. Пилки (1974), «Механика твёрдых тел» (книга)
- ^ Дональд Рэй Смит и Клиффорд Трусделл (1993) «Введение в механику сплошной среды после Трусделла и Нолла». Springer. ISBN 0-7923-2454-4
- ^ Фритьов Иргенс (2008), «Механика сплошных сред». Спрингер. ISBN 3-540-74297-2
- ^ Уильям С. Слотер (2012), «Линеаризованная теория упругости». Birkhäuser Basel ISBN 978-0-8176-4117-7
Дальнейшее чтение
- Чакрабарти, Дж. (2006). Теория пластичности (3-е изд.). Баттерворт-Хайнеманн. С. 17–32. ISBN 0-7506-6638-2.
- Бир, Фердинанд Пьер; Элвуд Рассел Джонстон; Джон Т. ДеВольф (1992). Механика материалов . McGraw-Hill Professional. ISBN 0-07-112939-1.
- Брэди, Б. Х. Г.; Э. Т. Браун (1993). Механика горных пород для подземной добычи (третье изд.). Kluwer Academic Publisher. стр. 17–29. ISBN 0-412-47550-2.
- Чен, Вай-Фа; Балади, Г.И. (1985). Пластичность почвы, теория и реализация . Elsevier Science. ISBN 0-444-42455-5.
- Chou, Pei Chi; Pagano, NJ (1992). Эластичность: тензорный, диадический и инженерный подходы. Книги Dover по инженерии. Dover Publications. стр. 1–33. ISBN 0-486-66958-0.
- Дэвис, РО; Селвадурай. APS (1996). Упругость и геомеханика. Cambridge University Press. С. 16–26. ISBN 0-521-49827-9.
- Дитер, GE (3-е изд.). (1989). Механическая металлургия . Нью-Йорк: McGraw-Hill. ISBN 0-07-100406-8 .
- Хольц, Роберт Д.; Ковач, Уильям Д. (1981). Введение в геотехническую инженерию. Серия по гражданскому строительству и инженерной механике издательства Prentice-Hall. Prentice-Hall. ISBN 0-13-484394-0.
- Джонс, Роберт Миллард (2008). Деформационная теория пластичности. Bull Ridge Corporation. С. 95–112. ISBN 978-0-9787223-1-9.
- Юмикис, Альфредс Р. (1969). Теоретическая механика грунтов: с практическими приложениями к механике грунтов и фундаментостроению. Van Nostrand Reinhold Co. ISBN 0-442-04199-3.
- Ландау, Л. Д. и Лифшиц Э. М. (1959). Теория упругости .
- Лав, AEH (4-е изд.). (1944). Трактат о математической теории упругости . Нью-Йорк: Dover Publications. ISBN 0-486-60174-9 .
- Марсден, Дж. Э.; Хьюз, Т. Дж. Р. (1994). Математические основы упругости . Dover Publications. стр. 132–142. ISBN 0-486-67865-2.
- Пэрри, Ричард Хоули Грей (2004). Круги Мора, пути напряжений и геотехника (2-е изд.). Тейлор и Фрэнсис. стр. 1–30. ISBN 0-415-27297-1.
- Рис, Дэвид (2006). Основы инженерной пластичности – Введение в инженерные и производственные приложения. Butterworth-Heinemann. С. 1–32. ISBN 0-7506-8025-3.
- Тимошенко, Стивен П.; Джеймс Норман Гудье (1970). Теория упругости (третье изд.). McGraw-Hill International Editions. ISBN 0-07-085805-5.
- Тимошенко, Стивен П. (1983). История сопротивления материалов: с кратким изложением истории теории упругости и теории структур. Dover Books on Physics. Dover Publications. ISBN 0-486-61187-6.


































