Пространство для гребня
В математике, в частности топологии , гребенчатое пространство — это особое подпространство , напоминающее гребенку . Гребенчатое пространство обладает свойствами, которые служат рядом контрпримеров . Синусоидальная кривая тополога имеет свойства, схожие с гребенчатым пространством. Удаленное гребенчатое пространство является вариацией гребенчатого пространства.
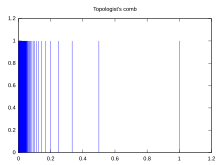

Формальное определение
Рассмотрим его стандартную топологию и пусть K будет множеством . Множество C определяется как:
рассматриваемое как подпространство, снабженное топологией подпространства, известно как гребенчатое пространство. Удаленное гребенчатое пространство, D, определяется как:
- .
Это пространство гребенки с удаленным сегментом линии.
Топологические свойства
Пространство гребенки и пространство удаленной гребенки обладают некоторыми интересными топологическими свойствами, в основном связанными с понятием связности .
1. Пространство гребенки C является линейно связным и стягиваемым , но не локально стягиваемым, локально линейно связным или локально связным.
2. Удаленное пространство гребенки, D, связано:
- Пусть E — пространство гребенки без . E также путевым образом связно, а замыкание E — пространство гребенки. Так как E D — замыкание E, где E связно, то удаленное пространство гребенки также связно.
3. Удаленное пространство гребенки не является путеводно связанным, поскольку нет пути из (0,1) в (0,0):
- Предположим, что существует путь из p = (0, 1) в точку (0, 0) в D . Пусть f : [0, 1] → D будет этим путем. Мы докажем, что f −1 { p } одновременно открыт и замкнут в [0, 1], что противоречит связности этого множества. Очевидно, что f −1 { p } замкнут в [0, 1] в силу непрерывности f . Чтобы доказать , что f −1 { p } открыт , мы действуем следующим образом: выбираем окрестность V (открытую в R 2 ) вокруг p , которая не пересекает ось x . Предположим , что x — произвольная точка в f −1 { p }. Очевидно, f ( x ) = p . Тогда, поскольку f −1 ( V ) открыт, существует базисный элемент U, содержащий x, такой, что f ( U ) является подмножеством V . Мы утверждаем, что f ( U ) = { p }, что будет означать, что U является открытым подмножеством f −1 { p }, содержащим x . Поскольку x был произвольным, f −1 { p } будет тогда открытым. Мы знаем, что U связно, поскольку оно является базисным элементом для топологии порядка на [0, 1]. Следовательно, f ( U ) связно. Предположим, что f ( U ) содержит точку s, отличную от p . Тогда s = (1/ n , z ) должно принадлежать D . Выберем r таким образом, чтобы 1/( n + 1) < r < 1/ n . Поскольку f ( U ) не пересекает ось x , множества A = (−∞, r ) × и B = ( r , +∞) × будут образовывать разделение на f ( U ); противоречащее связности f ( U ). Следовательно, f −1 { p } одновременно открыто и замкнуто в [0, 1]. Это противоречие.
4. Пространство гребенки гомотопно точке, но не допускает сильной деформации ретракции на точку для любого выбора базовой точки, лежащей в отрезке
Смотрите также
- Связанное пространство
- Пространство для ежа
- Бесконечная метла
- Список топологий
- Локально связанное пространство
- Топология заказа
- Синусоида тополога
Ссылки
- Джеймс Манкрес (1999). Топология (2-е изд.). Prentice Hall . ISBN 0-13-181629-2.
- Киёси Ито (ред.). «Связность». Энциклопедический словарь математики . Математическое общество Японии.


![{\displaystyle (\{0\}\times [0,1])\cup (K\times [0,1])\cup ([0,1]\times \{0\})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1840c5c3f77daef5355824188b1cc18ab96ebd57)
![{\displaystyle \{(0,1)\}\cup (K\times [0,1])\cup ([0,1]\times \{0\})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d52920ed9426c2722c09b6b2941b621a4f7a4b6d)

![{\displaystyle \{0\}\times (0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01c9697d05fbb7c7c383fea878ae14a4c7849e77)

