Сортировка гребнем

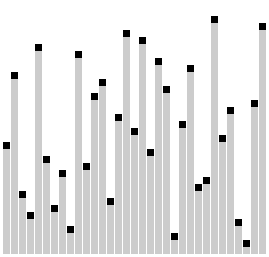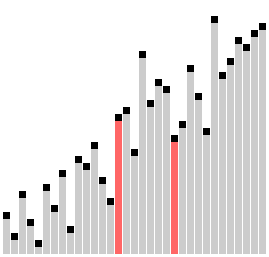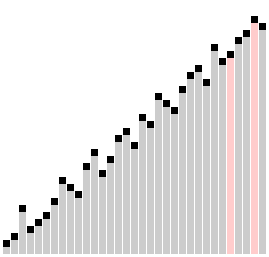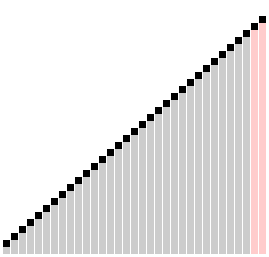Сортировка гребнем

Сортировка гребнем с коэффициентом сжатия k =1,24733
Сорт	Алгоритм сортировки
Структура данных	Множество
Худший вариант производительности	${\displaystyle O(n^{2})}$[1]
Лучшая производительность	${\displaystyle \Тета (n\log n)}$
Средняя производительность	${\displaystyle \Omega (n^{2}/2^{p})}$, где p — число приращений [1]
Наихудшая сложность пространства	${\displaystyle O(1)}$

Сортировка гребнем — сравнительно простой алгоритм сортировки , первоначально разработанный Влодзимежем Добосевичем и Артуром Боровым в 1980 году ^{[1] [2]} , позже переоткрытый (и получивший название «Сортировка гребнем») Стивеном Лэйси и Ричардом Боксом в 1991 году ^[3]. Сортировка гребнем улучшает пузырьковую сортировку таким же образом, как сортировка Шелла улучшает сортировку вставками , поскольку они оба позволяют элементам, которые изначально находятся далеко от своего предполагаемого положения, перемещаться более чем на одну позицию за одну замену.

В определении «сортировки с убывающим шагом» на nist.gov термин «сортировка гребнем» упоминается как визуализация итеративных проходов данных, «где зубья гребня соприкасаются»; первый термин связан с именем Дона Кнута . ^[4]

Основная идея заключается в том, чтобы исключить черепах , или небольшие значения около конца списка, поскольку в пузырьковой сортировке они сильно замедляют сортировку. Кролики , большие значения около начала списка, не представляют проблемы в пузырьковой сортировке.

В пузырьковой сортировке, когда сравниваются любые два элемента, они всегда имеют зазор (расстояние друг от друга), равный 1. ^[5] Основная идея сортировки гребнем заключается в том, что зазор может быть намного больше 1. Внутренний цикл пузырьковой сортировки, который фактически выполняет обмен , модифицируется таким образом, что зазор между обмениваемыми элементами уменьшается (для каждой итерации внешнего цикла) с шагом «коэффициента сжатия» k : [ ⁠н/к⁠ , ⁠н/к ²⁠ , ⁠н/к ³⁠ , ..., 1] .

Разрыв начинается с длины сортируемого списка n, деленной на коэффициент сжатия k (обычно 1,3; см. ниже), и один проход вышеупомянутой модифицированной пузырьковой сортировки применяется с этим разрывом. Затем разрыв снова делится на коэффициент сжатия, список сортируется с этим новым разрывом, и процесс повторяется до тех пор, пока разрыв не станет равным 1. На этом этапе сортировка гребенкой продолжает использовать разрыв 1, пока список не будет полностью отсортирован. Таким образом, заключительный этап сортировки эквивалентен пузырьковой сортировке, но к этому времени большинство черепах уже разобрались, поэтому пузырьковая сортировка будет эффективной.

Коэффициент сжатия оказывает большое влияние на эффективность сортировки гребнем. Добосевич предложил k = 4/3 = 1,333…, в то время как Лейси и Бокс предлагают 1,3 как идеальный коэффициент сжатия после эмпирического тестирования на более чем 200 000 случайных списках длиной около 1000. Слишком малое значение замедляет алгоритм, делая ненужно много сравнений, тогда как слишком большое значение не позволяет эффективно справляться с черепахами, из-за чего требуется много проходов с зазором 1.

Модель повторных проходов сортировки с уменьшающимися зазорами похожа на сортировку Шелла, но в сортировке Шелла массив полностью сортируется на каждом проходе, прежде чем перейти к следующему наименьшему зазору. Проходы сортировки гребенкой не полностью сортируют элементы. Это причина того, что последовательности зазоров сортировки Шелла имеют больший оптимальный коэффициент сжатия около 2,25.

Еще одно уточнение, предложенное Лейси и Боксом, — это «правило 11»: всегда используйте размер зазора 11, округляя размеры зазоров 9 или 10 (достигаемые путем деления зазоров 12, 13 или 14 на 1,3) до 11. Это исключает возможность выживания черепах до последнего прохода через зазор 1.

Функция combsort( входной массив ) — это gap := input.size // Инициализация размера зазора shrink := 1.3 // Установка коэффициента сжатия зазора сортировано := false цикл пока сортируется = false // Обновить значение зазора для следующего гребня зазор := пол(зазор / усадка) если зазор ≤ 1 , то разрыв := 1 sorted := true // Если в этом проходе нет обменов, то мы закончили,  иначе если gap = 9 или gap = 10 , то gap := 11 // "Правило 11"  заканчивается, если // Одинарная «гребёнка» по входному списку я := 0 цикл пока i + пробел < input.size // См. сортировку Шелла для похожей идеи  если input[i] > input[i+gap] тогда  поменяйте местами (input[i], input[i+gap]) сортировано := false // Если это назначение никогда не происходит внутри цикла, // тогда обменов не было и список отсортирован.  end if  я := я + 1 конец цикла  конец цикла конец функции

В Wikibook Algorithm Implementation есть страница по теме: Сортировка гребнем

• В основе сортировки расческой лежит пузырьковая сортировка , которая, как правило, является более медленным алгоритмом.
• Коктейльная сортировка , или двунаправленная пузырьковая сортировка, — это разновидность пузырьковой сортировки, которая также решает проблему черепах, хотя и менее эффективно.