Сложность схемы
Модель вычислительной сложности

Пример булевой схемы. Узлы — это вентили И , узлы — это вентили ИЛИ , а узлы — это вентили НЕ ∧ {\displaystyle \клин} ∨ {\displaystyle \vee} ¬ {\displaystyle \отрицательный}

В теоретической информатике сложность схемы — это раздел теории сложности вычислений , в котором булевы функции классифицируются в соответствии с размером или глубиной булевых схем , которые их вычисляют. Связанное понятие — сложность схемы рекурсивного языка , которая определяется однородным семейством схем (см. ниже). С 1 , С 2 , … {\displaystyle C_{1},C_{2},\ldots }

Доказательство нижних границ размера булевых схем, вычисляющих явные булевы функции, является популярным подходом к разделению классов сложности. Например, известный класс схем P/poly состоит из булевых функций, вычисляемых схемой полиномиального размера. Доказательство этого разделило бы P и NP (см. ниже). Н П ⊈ П / п о л у {\displaystyle {\mathsf {NP}}\not \subseteq {\mathsf {P/поли}}}

Классы сложности, определенные в терминах булевых схем, включают AC 0 , AC , TC 0 , NC 1 , NC и P/poly .

Размер и глубина

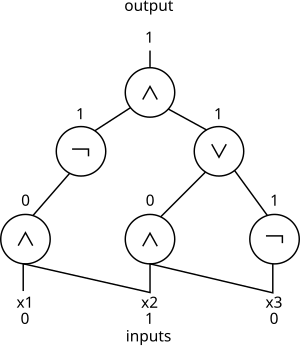
Булева схема с входными битами — это направленный ациклический граф , в котором каждый узел (обычно называемый в этом контексте вентилями ) является либо входным узлом входящей степени 0, помеченным одним из входных битов, вентилем И , вентилем ИЛИ или вентилем НЕ . Один из этих вентилей обозначается как выходной вентилем. Такая схема естественным образом вычисляет функцию своих входов. Размер схемы — это количество вентилей, которые она содержит, а ее глубина — это максимальная длина пути от входного вентиля до выходного вентиля. н {\displaystyle n} н {\displaystyle n} н {\displaystyle n}

Существует два основных понятия сложности схемы [1] Сложность размера схемы булевой функции — это минимальный размер любого вычисления схемы . Сложность глубины схемы булевой функции — это минимальная глубина любого вычисления схемы . ф {\displaystyle f} ф {\displaystyle f} ф {\displaystyle f} ф {\displaystyle f}

Эти понятия обобщаются, когда мы рассматриваем сложность схемы любого языка, который содержит строки с разной длиной бит, особенно бесконечные формальные языки . Булевы схемы, однако, допускают только фиксированное количество входных бит. Таким образом, ни одна булева схема не способна определить такой язык. Чтобы учесть эту возможность, мы рассматриваем семейства схем , где каждая принимает входные данные размера . Каждое семейство схем будет естественным образом генерировать язык с помощью выходных данных схемы , когда строка длины является членом семейства, и в противном случае. Мы говорим, что семейство схем имеет минимальный размер, если нет другого семейства, которое принимает решения о входных данных любого размера, , со схемой меньшего размера, чем (соответственно для семейств с минимальной глубиной ). Таким образом, сложность схемы имеет смысл даже для нерекурсивных языков . Понятие однородного семейства позволяет связать варианты сложности схемы с мерами сложности рекурсивных языков на основе алгоритмов. Однако неоднородный вариант полезен для нахождения нижних границ того, насколько сложным должно быть любое семейство схем, чтобы определить заданные языки. С 1 , С 2 , … {\displaystyle C_{1},C_{2},\ldots } С н {\displaystyle C_{n}} н {\displaystyle n} С н {\displaystyle C_{n}} 1 {\displaystyle 1} н {\displaystyle n} 0 {\displaystyle 0} н {\displaystyle n} С н {\displaystyle C_{n}}

Следовательно, сложность размера схемы формального языка определяется как функция , которая связывает длину входных данных в битах, , со сложностью размера схемы минимальной схемы , которая решает, находятся ли входные данные этой длины в . Сложность глубины схемы определяется аналогично. А {\displaystyle А} т : Н → Н {\displaystyle t:\mathbb {N} \to \mathbb {N} } н {\displaystyle n} С н {\displaystyle C_{n}} А {\displaystyle А}

Однородность

Булевы схемы являются одним из основных примеров так называемых неоднородных моделей вычислений в том смысле, что входные данные разной длины обрабатываются разными схемами, в отличие от однородных моделей, таких как машины Тьюринга , где одно и то же вычислительное устройство используется для всех возможных длин входных данных. Таким образом, отдельная вычислительная задача связана с определенным семейством булевых схем , где каждая представляет собой схему, обрабатывающую входные данные из n бит. Условие однородности часто накладывается на эти семейства, требуя существования некоторой, возможно, ограниченной по ресурсам машины Тьюринга, которая на входе n производит описание отдельной схемы . Когда эта машина Тьюринга имеет полиномиальное по n время выполнения , семейство схем называется P-однородным. Более строгое требование DLOGTIME -однородности представляет особый интерес при изучении классов схем малой глубины, таких как AC 0 или TC 0 . Если ограничения ресурсов не указаны, язык является рекурсивным (т.е. разрешимым машиной Тьюринга) тогда и только тогда, когда язык определяется однородным семейством булевых схем. С 1 , С 2 , … {\displaystyle C_{1},C_{2},\точки } С н {\displaystyle C_{n}} С н {\displaystyle C_{n}}

Равномерный полиномиальный по времени

Семейство булевых схем является однородным за полиномиальное время , если существует детерминированная машина Тьюринга M , такая, что { С н : н ∈ Н } {\displaystyle \{C_{n}:n\in \mathbb {N} \}}

  • M выполняется за полиномиальное время
  • Для всех M выводит описание на входе н ∈ Н {\displaystyle n\in \mathbb {N} } С н {\displaystyle C_{n}} 1 н {\displaystyle 1^{н}}

Униформа Logspace

Семейство булевых схем является однородным по логарифмическому пространству , если существует детерминированная машина Тьюринга M , такая, что { С н : н ∈ Н } {\displaystyle \{C_{n}:n\in \mathbb {N} \}}

История

Сложность схем восходит к Шеннону в 1949 году [2], который доказал, что почти все булевы функции от n переменных требуют схем размера Θ(2 n / n ). Несмотря на этот факт, теоретики сложности до сих пор не смогли доказать сверхлинейную нижнюю границу для какой-либо явной функции.

Суперполиномиальные нижние границы были доказаны при определенных ограничениях на семейство используемых схем. Первой функцией, для которой были показаны суперполиномиальные нижние границы схем, была функция четности , которая вычисляет сумму своих входных битов по модулю 2. Тот факт, что четность не содержится в AC 0, был впервые независимо установлен Айтаем в 1983 году [3] [4] и Фурстом, Саксе и Сипсером в 1984 году. [5] Более поздние усовершенствования Хостада в 1987 году [6] установили, что любое семейство схем постоянной глубины, вычисляющих функцию четности, требует экспоненциального размера. Расширяя результат Разборова [7], Смоленский в 1987 году [8] доказал, что это верно, даже если схема дополнена вентилями, вычисляющими сумму своих входных битов по модулю некоторого нечетного простого числа p .

Задача о k -клике заключается в том, чтобы решить, имеет ли заданный граф на n вершинах клику размера k . Для любого конкретного выбора констант n и k граф может быть закодирован в двоичном виде с использованием битов, которые указывают для каждого возможного ребра, присутствует ли оно. Затем задача о k -клике формализуется как функция , которая выводит 1 тогда и только тогда, когда граф, закодированный строкой, содержит клику размера k . Это семейство функций является монотонным и может быть вычислено семейством схем, но было показано, что его нельзя вычислить семейством монотонных схем полиномиального размера (то есть схемами с вентилями И и ИЛИ, но без отрицания). Первоначальный результат Разборова 1985 года [7] был позже улучшен до нижней границы экспоненциального размера Алоном и Боппаной в 1987 году. [9] В 2008 году Россман [10] показал, что схемы постоянной глубины с вентилями И, ИЛИ и НЕ требуют размера для решения проблемы k -клики даже в среднем случае . Более того, существует схема размера , которая вычисляет . ( н 2 ) {\displaystyle {n \выберите 2}} ф к : { 0 , 1 } ( н 2 ) → { 0 , 1 } {\displaystyle f_{k}:\{0,1\}^{n \выберите 2}\to \{0,1\}} ф к {\displaystyle f_{k}} Ω ( н к / 4 ) {\displaystyle \Омега (n^{k/4})} н к / 4 + О ( 1 ) {\displaystyle n^{k/4+O(1)}} ф к {\displaystyle f_{k}}

В 1999 году Раз и Маккензи показали, что монотонная иерархия NC бесконечна. [11]

Задача о целочисленном делении лежит в однородном TC 0 . [12]

Нижние границы схемы

Нижние границы схемы обычно сложны. Известные результаты включают

  • Четность не существует в неоднородном AC 0 , что доказал Аджтай в 1983 году [3] [4] , а также Фурст, Сакс и Сипсер в 1984 году [5].
  • Единый TC 0 строго содержится в PP , доказано Аллендером. [13]
  • Классы SП
    2    , PP [nb 1] и MA /1 [14] (MA с одним советом) не находятся в SIZE ( n k ) ни для какой константы k.
  • Хотя есть подозрение, что неоднородный класс ACC 0 не содержит функцию большинства, только в 2010 году Уильямс доказал это . [15] Н Э Х П ⊈ А С С 0 {\displaystyle {\mathsf {NEXP}}\not \subseteq {\mathsf {ACC}}^{0}}

Открытым остается вопрос о том, имеет ли NEXPTIME неоднородные цепи TC 0 .

Доказательства нижних границ схем тесно связаны с дерандомизацией . Доказательство, которое подразумевает, что либо , либо этот перманент не может быть вычислен неоднородными арифметическими схемами (многочленами) полиномиального размера и полиномиальной степени. [16] П = Б П П {\displaystyle {\mathsf {P}}={\mathsf {BPP}}} Н Э Х П ⊈ П / п о л у {\displaystyle {\mathsf {NEXP}}\not \subseteq {\mathsf {P/поли}}}

В 1997 году Разборов и Рудич показали, что многие известные нижние границы схем для явных булевых функций подразумевают существование так называемых естественных свойств, полезных против соответствующего класса схем. [17] С другой стороны, естественные свойства, полезные против P/poly, сломали бы сильные псевдослучайные генераторы. Это часто интерпретируется как барьер «естественных доказательств» для доказательства сильных нижних границ схем. В 2016 году Кармосино, Импальяццо, Кабанец и Колоколова доказали, что естественные свойства также могут быть использованы для построения эффективных алгоритмов обучения. [18]

Классы сложности

Многие классы сложности схем определяются в терминах иерархий классов. Для каждого неотрицательного целого числа i существует класс NC i , состоящий из схем полиномиального размера глубины , использующих ограниченные вентили AND, OR и NOT с вентилями ... О ( бревно я ⁡ ( н ) ) {\displaystyle O(\log ^{i}(n))}

Отношение к временной сложности

Если определенный язык, , принадлежит к классу временной сложности для некоторой функции , то имеет сложность схемы . Если машина Тьюринга, которая принимает язык, забывчива (что означает, что она читает и записывает одни и те же ячейки памяти независимо от ввода), то имеет сложность схемы . [19] А {\displaystyle А} ВРЕМЯ ( т ( н ) ) {\displaystyle {\text{ВРЕМЯ}}(t(n))} т : Н → Н {\displaystyle t:\mathbb {N} \to \mathbb {N} } А {\displaystyle А} О ( т ( н ) бревно ⁡ т ( н ) ) {\displaystyle {\mathcal {O}}(t(n)\log t(n))} А {\displaystyle А} О ( т ( н ) ) {\displaystyle {\mathcal {O}}(t(n))}

Монотонные схемы

Монотонная булева схема — это схема, которая имеет только вентили И и ИЛИ, но не имеет вентилей НЕ. Монотонная схема может вычислять только монотонную булеву функцию, которая является функцией, где для каждого , , где означает, что для всех . ф : { 0 , 1 } н → { 0 , 1 } {\displaystyle f:\{0,1\}^{n}\to \{0,1\}} х , у ∈ { 0 , 1 } н {\displaystyle x,y\in \{0,1\}^{n}} х ≤ у ⟹ ф ( х ) ≤ ф ( у ) {\displaystyle x\leq y\подразумевает f(x)\leq f(y)} х ≤ у {\displaystyle x\leq y} х я ≤ у я {\displaystyle x_{i}\leq y_{i}} я ∈ { 1 , … , н } {\displaystyle i\in \{1,\ldots ,n\}}

Смотрите также

Примечания

  1. ^ См . доказательство .

Ссылки

  1. ^ Сипсер, Майкл (1997). Введение в теорию вычислений (1-е изд.). Бостон, США: PWS Publishing Company. стр. 324.
  2. ^ Шеннон, Клод Элвуд (1949). «Синтез двухполюсных коммутационных схем». Bell System Technical Journal . 28 (1): 59–98. doi :10.1002/j.1538-7305.1949.tb03624.x.
  3. ^ ab Ajtai, Miklós (1983). " -формулы на конечных структурах". Annals of Pure and Applied Logic . 24 : 1–24. doi :10.1016/0168-0072(83)90038-6. Σ 1 1 {\displaystyle \Sigma _{1}^{1}}
  4. ^ аб Айтай, Миклош ; Комлос, Янош ; Семереди, Эндре (1983). « Сортировочная сеть». Материалы 15-го ежегодного симпозиума ACM по теории вычислений, 25–27 апреля 1983 г., Бостон, Массачусетс, США . Ассоциация вычислительной техники. стр. 1–9. дои : 10.1145/800061.808726. О ( н бревно ⁡ н ) {\displaystyle O(n\log n)}
  5. ^ ab Furst, Merrick L.; Saxe, James Benjamin ; Sipser, Michael Fredric (1984). «Четность, схемы и иерархия полиномиального времени». Математическая теория систем . 17 (1): 13–27. doi :10.1007/BF01744431. MR  0738749. S2CID  6306235.
  6. ^ Хастад, Йохан Торкель (1987). Вычислительные ограничения схем малой глубины (PDF) (диссертация). Массачусетский технологический институт.
  7. ^ аб Разборов, Александр Александрович (1985). «Нижние оценки монотонной сложности некоторых булевых функций». Советская математика — Доклады . 31 : 354–357. ISSN  0197-6788.
  8. ^ Смоленский, Роман (1987). «Алгебраические методы в теории нижних оценок сложности булевых схем». Труды 19-го ежегодного симпозиума ACM по теории вычислений . Ассоциация вычислительной техники . С. 77–82. doi : 10.1145/28395.28404 .
  9. ^ Алон, Нога ; Боппана, Рави Б. (1987). «Монотонная сложность схемы булевых функций». Комбинаторика . 7 (1): 1–22. CiteSeerX 10.1.1.300.9623 . дои : 10.1007/bf02579196. S2CID  17397273. 
  10. ^ Россман, Бенджамин Э. (2008). «О постоянной глубине сложности k-клики». STOC 2008: Труды 40-го ежегодного симпозиума ACM по теории вычислений . Ассоциация вычислительной техники . С. 721–730. doi :10.1145/1374376.1374480.
  11. ^ Раз, Ран ; Маккензи, Пьер (1999). «Разделение монотонной иерархии NC». Combinatorica . 19 (3): 403–435. doi :10.1007/s004930050062.
  12. ^ Гессе, Уильям (2001). «Разделение в форме TC 0 ». Труды 28-го Международного коллоквиума по автоматам, языкам и программированию . Springer Verlag . С. 104–114.
  13. ^ Аллендер, Эрик (1996). «Сложность схем перед рассветом нового тысячелетия». В Чандру, Виджай; Винай, В. (ред.). Основы программных технологий и теоретической информатики, 16-я конференция, Хайдарабад, Индия, 18–20 декабря 1996 г., Труды . Заметки лекций по информатике. Том 1180. Springer. стр. 1–18. doi :10.1007/3-540-62034-6_33.
  14. ^ Сантханам, Рахул (2007). «Нижние границы цепей для классов Мерлина-Артура». STOC 2007: Труды тридцать девятого ежегодного симпозиума ACM по теории вычислений . С. 275–283. CiteSeerX 10.1.1.92.4422 . doi :10.1145/1250790.1250832. 
  15. ^ Уильямс, Ричард Райан (2011). «Нижние границы неоднородных схем ACC» (PDF) . CCC 2011: Труды 26-й ежегодной конференции IEEE по вычислительной сложности . стр. 115–125. doi :10.1109/CCC.2011.36.
  16. ^ Кабанец, Валентин; Импальяццо, Рассел Грэм (2004). «Дерандомизация полиномиальных тестов идентичности означает доказательство нижних границ схемы». Computational Complexity . 13 (1): 1–46. doi :10.1007/s00037-004-0182-6. S2CID  12451799.
  17. ^ Разборов, Александр Александрович ; Рудич, Стивен (1997). «Естественные доказательства». Журнал компьютерных и системных наук . Т. 55. С. 24–35.
  18. ^ Кармосино, Марко; Импальяццо, Рассел Грэм ; Кабанец, Валентин; Колоколова, Антонина (2016). «Изучение алгоритмов на основе естественных доказательств». Computational Complexity Conference .
  19. ^ Пиппенджер, Николас ; Фишер, Майкл Дж. (1979). «Связи между мерами сложности». Журнал ACM . 26 (3): 361–381. doi : 10.1145/322123.322138 . S2CID  2432526.

Дальнейшее чтение

  • Vollmer, Heribert [на немецком языке] (1999). Введение в сложность схем: единый подход . Тексты по теоретической информатике. Серия EATCS. ​​Springer Verlag . ISBN 978-3-540-64310-4.
  • Вегенер, Инго (1987) [ноябрь 1986 г.]. Сложность булевых функций . Серия Уайли – Тойбнера по компьютерным наукам. Франкфурт-на-Майне/Билефельд, Германия: John Wiley & Sons Ltd. и BG Teubner Verlag , Штутгарт. ISBN 3-519-02107-2. LCCN  87-10388.(xii+457 страниц) (Примечание. В то время влиятельный учебник по предмету, широко известный как «Синяя книга». Также доступен для скачивания (PDF) на Electronic Colloquium on Computational Complexity .)
  • Цвик, Ури . «Конспект лекций по курсу Ури Цвика по сложности схем».
Взято с "https://en.wikipedia.org/w/index.php?title=Сложность_цепи&oldid=1248087402"