каталонский номер

Рекурсивная целочисленная последовательность

Числа Каталана — это последовательность натуральных чисел , которые встречаются в различных задачах подсчета , часто включающих рекурсивно определенные объекты. Они названы в честь Эжена Каталана , хотя были ранее открыты в 1730-х годах Минггату .

Число Каталана $n$ можно выразить непосредственно через центральные биномиальные коэффициенты следующим образом:

C_{n}={\frac {1}{n+1}}{2n \choose n}={\frac {(2n)!}{(n+1)!\,n!}}\qquad {\text{for }}n\geq 0.

Первые каталонские числа для $n = 0, 1, 2, 3, ...$ равны

1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, ...

(последовательность A000108 в OEIS ).

Характеристики

Альтернативное выражение для $C n$ :

C_{n}={2n \выберите n}-{2n \выберите n+1}

для

n\geq 0\,,

что эквивалентно выражению, данному выше, поскольку . Это выражение показывает, что $C$ $n$ является целым числом , что не сразу очевидно из первой приведенной формулы. Это выражение составляет основу для доказательства правильности формулы. ${\tbinom {2n}{n+1}}={\tfrac {n}{n+1}}{\tbinom {2n}{n}}$

Другое альтернативное выражение —

C_{n}={\frac {1}{2n+1}}{2n+1 \выберите n}\,,

что можно непосредственно интерпретировать в терминах леммы о цикле ; см. ниже.

Числа Каталана удовлетворяют рекуррентным соотношениям

C_{0}=1\quad {\text{и}}\quad C_{n}=\sum _{i=1}^{n}C_{i-1}C_{ni}\quad {\text{для }}n>0

и

C_{0}=1\quad {\text{и}}\quad C_{n}={\frac {2(2n-1)}{n+1}}C_{n-1}\quad {\text{для }}n>0.

Асимптотически числа Каталана растут в том смысле, что частное $n$ -го числа Каталана и выражения справа стремится к 1, когда $n$ стремится к бесконечности. $C_{n}\sim {\frac {4^{n}}{n^{3/2}{\sqrt {\pi }}}}\,,$

Это можно доказать, используя асимптотический рост центральных биномиальных коэффициентов , приближение Стирлинга для или с помощью производящих функций . $н!$

Единственные каталонские числа $C n ,$ которые являются нечетными, это те, для которых $n = 2 k - 1$ ; все остальные четные. Единственные простые каталонские числа - это $C 2 = 2$ и $C 3 = 5$ . ^[1] В более общем смысле, кратность, с которой простое число $p$ делит $C n ,$ можно определить, сначала выразив $n + 1$ в основании $p$ . Для $p = 2$ кратность - это количество бит 1 минус 1. Для $p$ нечетного простого числа, подсчитайте все цифры, большие, чем $(p + 1) / 2$ ; также подсчитайте цифры, равные $(p + 1) / 2$ , если они не конечные; и подсчитайте цифры, равные $(p - 1) / 2 ,$ если они не конечные, и подсчитайте следующую цифру. ^[2] Единственные известные нечетные каталонские числа, которые не имеют последней цифры 5, это $C 0 = 1$ , $C 1 = 1$ , $C 7 = 429$ , $C 31$ , $C 127$ и $C 255.$ Нечетные каталонские числа, $C n$ для $n = 2 k - 1$ , не имеют последней цифры 5, если $n + 1$ имеет представление с основанием 5, содержащее только 0, 1 и 2, за исключением наименее значимого разряда, который также может быть 3. ^[3]

Числа Каталана имеют интегральные представления ^[4]^[5]

C_{n}={\frac {1}{2\pi}}\int _{0}^{4}x^{n}{\sqrt {\frac {4-x}{x}}}\,dx\,={\frac {2}{\pi}}4^{n}\int _{-1}^{1}t^{2n}{\sqrt {1-t^{2}}}\,dt.

что немедленно приводит к . $\sum _{n=0}^{\infty }{\frac {C_{n}}{4^{n}}}=2$

Это имеет простую вероятностную интерпретацию. Рассмотрим случайное блуждание по целочисленной прямой, начинающееся с 0. Пусть -1 будет состоянием "ловушки", таким, что если идущий прибудет в -1, он останется там. Идущий может прибыть в состояние ловушки в моменты времени 1, 3, 5, 7..., а число способов, которыми идущий может прибыть в состояние ловушки в момент времени, равно . Поскольку одномерное случайное блуждание является рекуррентным, вероятность того, что идущий в конечном итоге прибудет в -1, равна . $2k+1$ $C_{k}$ $\sum _{n=0}^{\infty }{\frac {C_{n}}{2^{2n+1}}}=1$

Приложения в комбинаторике

В комбинаторике существует множество задач на подсчет, решение которых дается числами Каталонии. Книга «Перечислительная комбинаторика: Том 2» комбинаториста Ричарда П. Стэнли содержит набор упражнений, описывающих 66 различных интерпретаций чисел Каталонии. Ниже приведены некоторые примеры с иллюстрациями случаев $C 3 = 5$ и $C 4 = 14$ .

$C n$ — это число слов Дика ^[6] длины $2 n$ . Слово Дика — это строка, состоящая из $n$ X и $n$ Y, такая, что ни один начальный сегмент строки не содержит больше Y, чем X. Например, ниже приведены слова Дика длиной до 6:

ИКСИ

XXYY XYXY

XXXYYY XYXXYY XYXYXY XXYYXY XXYXYY

Переосмысливая символ X как открывающую скобку , а Y как закрывающую скобку, $C n$ подсчитывает количество выражений, содержащих $n$ пар скобок, которые сопоставлены правильно:

((())) (()()) (())() ()(()) ()()()

$C n$ — это число различных способов, которыми $n + 1$ множители могут быть полностью заключены в скобки (или число способов связать $n$ применений бинарного оператора , как в задаче умножения цепочки матриц ). Например, для $n = 3$ у нас есть следующие пять различных заключений в скобки четырех множителей:

((аб)в)г (а(бв))г (аб)(вг) а((бв)г) а(б(вг))

Последовательные применения бинарного оператора можно представить в виде полного бинарного дерева , обозначив каждый лист $a, b, c, d$ . Отсюда следует, что $C n$ — это число полных бинарных деревьев с $n + 1$ листом или, что эквивалентно, с общим числом внутренних узлов $n$ :

$C n$ — число неизоморфных упорядоченных (или плоских) деревьев с $n + 1$ вершиной.^[7] См. кодирование общих деревьев как бинарных деревьев . Например, $C n$ — число возможных деревьев разбора для предложения (предполагая бинарное ветвление) при обработке естественного языка.
$C n$ — число монотонных решетчатых путей вдоль краев сетки с $квадратными ячейками n \times n$ , которые не выходят за пределы диагонали. Монотонный путь — это путь, который начинается в нижнем левом углу, заканчивается в верхнем правом углу и полностью состоит из краев, направленных вправо или вверх. Подсчет таких путей эквивалентен подсчету слов Дика: X означает «двигаться вправо», а Y означает «двигаться вверх».

На следующих диаграммах показан случай $n = 4$ :

Это можно представить, перечислив каталонские элементы по высоте столбца: ^[8]

[0,0,0,0] [0,0,0,1] [0,0,0,2] [0,0,1,1]

[0,1,1,1] [0,0,1,2] [0,0,0,3] [0,1,1,2] [0,0,2,2] [0,0,1,3]

[0,0,2,3] [0,1,1,3] [0,1,2,2] [0,1,2,3]

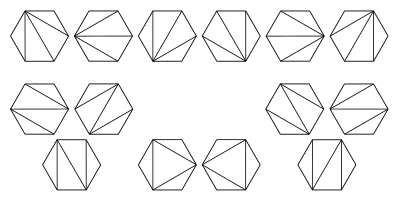
Выпуклый многоугольник с $n + 2$ сторонами можно разрезать на треугольники , соединив вершины непересекающимися отрезками прямых (форма триангуляции многоугольника ). Количество образованных треугольников равно $n$ , а количество различных способов, которыми это можно сделать, равно $C n$ . Следующие шестиугольники иллюстрируют случай $n = 4$ :

$C n$ — числосортируемых стеком перестановок { $1, ..., n}$ . Перестановка $w$ называется сортируемой стеком, если $S (w) = (1, ..., n)$ , где $S (w)$ определяется рекурсивно следующим образом: записываем $w = unv$ , где $n$ — наибольший элемент в $w$ , а $u$ и $v$ — более короткие последовательности, и устанавливаем $S (w) = S (u) S (v) n$ , где $S$ — тождество для последовательностей из одного элемента.
$C n$ — это число перестановок ${1, ..., n}$ , которые избегают шаблона перестановки 123 (или, альтернативно, любого из других шаблонов длины 3); то есть число перестановок без трехчленной возрастающей подпоследовательности. Для $n = 3$ эти перестановки равны 132, 213, 231, 312 и 321. Для $n = 4$ они равны 1432, 2143, 2413, 2431, 3142, 3214, 3241, 3412, 3421, 4132, 4213, 4231, 4312 и 4321.
$C n$ — число непересекающихся разбиений множества { $1, ..., n}$ . Тем более C $n никогда$ не превышает $n$ -го числа Белла . $C n$ — также число непересекающихся разбиений множества ${1, ..., 2 n}$ , в которых каждый блок имеет размер 2.
$C n$ — это количество способов замостить ступенчатую форму высотой $n$ прямоугольниками $n$ . Разрезание по антидиагонали и рассмотрение только ребер дает полные бинарные деревья. Следующий рисунок иллюстрирует случай $n = 4$ :

$C n$ — это количество способов сформировать «горный хребет» с $n$ восходящими и $n$ нисходящими штрихами, которые все остаются выше горизонтальной линии. Интерпретация горного хребта заключается в том, что горы никогда не опустятся ниже горизонта.

Горные хребты
$n=0:$	*	1 способ
$n=1:$	/\	1 способ
$n=2:$	/\ /\/\, / \	2 способа
$n=3:$	/ / / /\/\ / \ /\/\/\, /\/ \ , / \/\ , / \, / \	5 способов

$C n$ — это число стандартных таблиц Юнга, диаграмма которых представляет собой прямоугольник 2 на $n$ . Другими словами, это число способов, которыми числа $1, 2, ..., 2 n$ могут быть расположены в прямоугольнике 2 на $n$ так, чтобы каждая строка и каждый столбец увеличивались. Таким образом, формула может быть выведена как частный случай формулы длины крючка .

123 124 125 134 135456 356 346 256 246

$C_{n}$ — это число последовательностей длины $n$ , которые начинаются с , и могут увеличиваться либо на , либо на , либо уменьшаться на любое число (по крайней мере до ). Для них . Из пути Дика начните счетчик с $0$ . X увеличивает счетчик на $1$ , а Y уменьшает его на $1$ . Запишите значения только под X. По сравнению с аналогичным представлением чисел Белла , отсутствует только . $1$ $0$ $1$ $1$ $n=4$ $1234,1233,1232,1231,1223,1222,1221,1212,1211,1123,1122,1121,1112,1111$ $1213$

Доказательство формулы

Есть несколько способов объяснить, почему формула

C_{n}={\frac {1}{n+1}}{2n \выберите n}

решает комбинаторные задачи, перечисленные выше. Первое доказательство ниже использует производящую функцию . Другие доказательства являются примерами биективных доказательств ; они включают в себя буквальное подсчет коллекции некоторого вида объектов для получения правильной формулы.

Первое доказательство

Сначала заметим, что все перечисленные выше комбинаторные задачи удовлетворяют рекуррентному соотношению Сегнера ^[9]

C_{0}=1\quad {\text{и}}\quad C_{n+1}=\sum _{i=0}^{n}C_{i}\,C_{ni}\quad {\text{для }}n\geq 0.

Например, каждое слово Дика $w$ длины ≥ 2 можно записать единственным образом в виде

ш = X ш 1 Y ш 2

с (возможно пустыми) словами Дика $w 1$ и $w 2$ .

Производящая функция для каталонских чисел определяется как

c(x)=\sum _{n=0}^{\infty }C_{n}x^{n}.

Рекуррентное соотношение, приведенное выше, можно затем суммировать в форме производящей функции с помощью соотношения

с(х)=1+хс(х)^{2};

Другими словами, это уравнение следует из рекуррентного соотношения путем разложения обеих сторон в степенной ряд . С одной стороны, рекуррентное соотношение однозначно определяет числа Каталана; с другой стороны, интерпретируя $xc 2 - c + 1 = 0$ как квадратное уравнение c и используя квадратную формулу , соотношение производящей функции может быть алгебраически решено, чтобы получить два возможных $решения$

c(x)={\frac {1+{\sqrt {1-4x}}}{2x}}

или .

c(x)={\frac {1-{\sqrt {1-4x}}}{2x}}

Из двух возможностей следует выбрать вторую, поскольку только вторая дает

C_{0}=\lim _{x\to 0}c(x)=1

.

Квадратный корень можно разложить в степенной ряд, используя биномиальный ряд

${\begin{aligned}1-{\sqrt {1-4x}}&=-\sum _{n=1}^{\infty }{\binom {1/2}{n}}(-4x)^{n}=-\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}(2n-3)!!}{2^{n}n!}}(-4x)^{n}\\&=-\sum _{n=0}^{\infty }{\frac {(-1)^{n}(2n-1)!!}{2^{n+1}(n+1)!}}(-4x)^{n+1}=\sum _{n=0}^{\infty }{\frac {2^{n+1}(2n-1)!!}{(n+1)!}}x^{n+1}\\&=\sum _{n=0}^{\infty }{\frac {2(2n)!}{(n+1)!n!}}x^{n+1}=\sum _{n=0}^{\infty }{\frac {2}{n+1}}{\binom {2n}{n}}x^{n+1}\,.\end{aligned}}$ Таким образом, $c(x)={\frac {1-{\sqrt {1-4x}}}{2x}}=\sum _{n=0}^{\infty }{\frac {1}{n+1}}{\binom {2n}{n}}x^{n}\,.$

Второе доказательство

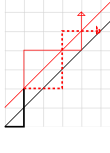
Подсчитываем количество путей, начинающихся и заканчивающихся на диагонали сетки $n \times n$ . Все такие пути имеют $n$ правых и $n$ верхних ступеней. Поскольку мы можем выбрать, какие из $2 n$ ступеней вверх или вправо, всего существует монотонных путей этого типа. Плохой путь пересекает главную диагональ и касается следующей более высокой диагонали (красной на иллюстрации). ${\tbinom {2n}{n}}$

Часть пути после более высокой диагонали затем переворачивается относительно этой диагонали, как показано красной пунктирной линией. Это меняет местами все правые шаги на верхние и наоборот. В той части пути, которая не отражается, есть на один верхний шаг больше, чем правых шагов, поэтому оставшаяся часть плохого пути имеет на один правый шаг больше, чем верхних шагов. Когда эта часть пути отражается, она будет иметь на один верхний шаг больше, чем правых шагов.

Поскольку все еще есть $2 n$ шагов, теперь есть $n + 1$ шагов вверх и $n - 1$ шагов вправо. Таким образом, вместо достижения $(n, n)$ все плохие пути после отражения заканчиваются в $(n - 1, n + 1)$ . Поскольку каждый монотонный путь в сетке $(n - 1) \times (n + 1)$ встречается с более высокой диагональю, и поскольку процесс отражения обратим, отражение, следовательно, является биекцией между плохими путями в исходной сетке и монотонными путями в новой сетке.

Таким образом, число плохих путей равно:

{n-1+n+1 \choose n-1}={2n \choose n-1}={2n \choose n+1}

а число каталонских путей (т.е. хороших путей) получается путем удаления числа плохих путей из общего числа монотонных путей исходной сетки,

C_{n}={2n \choose n}-{2n \choose n+1}={\frac {1}{n+1}}{2n \choose n}.

В терминах слов Дика мы начинаем с (недиковской) последовательности из $n$ X и $n$ Y и меняем местами все X и Y после первого Y, который нарушает условие Дика. После этого Y, обратите внимание, что Y ровно на один больше, чем X.

Третье доказательство

Это биективное доказательство дает естественное объяснение для термина $n + 1$ , появляющегося в знаменателе формулы для $C n$ . Обобщенную версию этого доказательства можно найти в статье Рукавицкой Йозеф (2011). ^[10]

При наличии монотонного пути превышение пути определяется как число вертикальных ребер над диагональю. Например, на рисунке 2 ребра над диагональю отмечены красным, поэтому превышение этого пути равно 5.

Для монотонного пути, превышение которого не равно нулю, мы применяем следующий алгоритм для построения нового пути, превышение которого на $1$ меньше, чем у того, с которого мы начали.

Начиная с левого нижнего угла, следуйте по траектории, пока она впервые не окажется выше диагонали.
Продолжайте следовать по пути, пока он снова не коснется диагонали. Обозначим через $X$ первое такое ребро, которое будет достигнуто.
Поменяйте местами часть пути, находящуюся до $X$ , с частью, находящейся после $X.$

На рисунке 3 черная точка указывает на точку, где путь впервые пересекает диагональ. Черный край — это $X$ , и мы размещаем последнюю точку решетки красной части в правом верхнем углу, а первую точку решетки зеленой части — в левом нижнем углу, и размещаем X соответственно, чтобы создать новый путь, показанный на второй диаграмме.

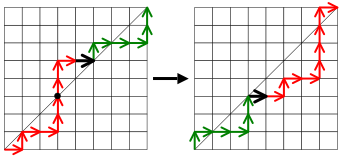
Рисунок 3. Зеленая и красная части меняются местами.

Превышение снизилось с $3$ до $2.$ Фактически, алгоритм уменьшает превышение на $1$ для любого пути, который мы ему подаём, потому что первый вертикальный шаг, начинающийся на диагонали (в точке, отмеченной чёрной точкой), является единственным вертикальным ребром, которое меняется с нахождения выше диагонали на нахождение ниже неё, когда мы применяем алгоритм — все остальные вертикальные ребра остаются по одну сторону от диагонали.

Рисунок 4. Все монотонные пути в сетке 3×3, иллюстрирующие алгоритм снижения превышения.

Видно, что этот процесс обратим : если задан любой путь $P$ , превышение которого меньше $n$ , то существует ровно один путь, который дает $P$ , когда к нему применяется алгоритм. Действительно, (черное) ребро $X$ , которое изначально было первым горизонтальным шагом, заканчивающимся на диагонали, стало последним горизонтальным шагом, начинающимся на диагонали. В качестве альтернативы можно обратить исходный алгоритм, чтобы найти первое ребро, проходящее ниже диагонали.

Это означает, что число путей превышения $n$ равно числу путей превышения $n - 1$ , которое равно числу путей превышения $n - 2$ , и так далее, вплоть до нуля. Другими словами, мы разбили множество всех монотонных путей на $n + 1$ классов одинакового размера, соответствующих возможным превышениям между 0 и $n$ . Поскольку существуют монотонные пути, мы получаем искомую формулу $\textstyle {2n \choose n}$ $\textstyle C_{n}={\frac {1}{n+1}}{2n \choose n}.$

Рисунок 4 иллюстрирует ситуацию для $n = 3.$ Каждый из 20 возможных монотонных путей появляется где-то в таблице. Первый столбец показывает все пути превышения три, которые лежат полностью выше диагонали. Столбцы справа показывают результат последовательного применения алгоритма, причем превышение уменьшается на одну единицу за раз. Имеется пять строк, то есть $C 3 = 5$ , а последний столбец отображает все пути не выше диагонали.

Используя слова Дика, начните с последовательности из . Пусть будет первым $X$ , который приводит исходную подпоследовательность к равенству, и сконфигурируйте последовательность как . Новая последовательность — . $\textstyle {\binom {2n}{n}}$ $X_{d}$ $(F)X_{d}(L)$ $LXF$

Четвертое доказательство

В этом доказательстве используется триангуляционное определение чисел Каталана для установления связи между $C n$ и $C n +1$ .

Дан многоугольник $P$ с $n + 2$ сторонами и триангуляцией, отметьте одну из его сторон как основание, а также сориентируйте одно из его $2 n + 1$ общих ребер. Для данного основания существует $(4 n + 2) C n таких отмеченных триангуляций.$

Дан многоугольник $Q$ с $n + 3$ сторонами и (другой) триангуляцией, снова отметьте одну из его сторон как основание. Отметьте одну из сторон, отличную от стороны основания (и не внутреннее ребро треугольника). Для данного основания существует $(n + 2) C n + 1$ таких отмеченных триангуляций.

Между этими двумя отмеченными триангуляциями существует простая биекция: мы можем либо свернуть треугольник в $Q$ , сторона которого отмечена (двумя способами, и вычесть два, которые не могут свернуть основание), либо, наоборот, расширить ориентированное ребро в $P$ до треугольника и отметить его новую сторону.

Таким образом

(4n+2)C_{n}=(n+2)C_{n+1}

.

Писать $\textstyle {\frac {4n-2}{n+1}}C_{n-1}=C_{n}.$

Потому что

(2n)!=(2n)!!(2n-1)!!=2^{n}n!(2n-1)!!

у нас есть

{\frac {(2n)!}{n!}}=2^{n}(2n-1)!!=(4n-2)!!!!.

Применение рекурсии дает результат. $C_{0}=1$

Пятое доказательство

Это доказательство основано на интерпретации слов Дика каталонских чисел, как и число способов правильно сопоставить $n$ пар скобок. Мы обозначаем (возможно, пустую) правильную строку с помощью $c$ , а ее обратную — с помощью $c'$ . Поскольку любое $c$ можно однозначно разложить на , суммирование по возможным длинам немедленно дает рекурсивное определение $C_{n}$ $c=(c_{1})c_{2}$ $c_{1}$

C_{0}=1\quad {\text{and}}\quad C_{n+1}=\sum _{i=0}^{n}C_{i}\,C_{n-i}\quad {\text{for }}n\geq 0

.

Пусть $b$ — сбалансированная строка длины $2 n$ , т.е. $b$ содержит одинаковое количество и , поэтому . Сбалансированную строку также можно однозначно разложить на либо , поэтому $($ $)$ $\textstyle B_{n}={2n \choose n}$ $(c)b$ $)c'(b$

B_{n+1}=2\sum _{i=0}^{n}B_{i}C_{n-i}.

Любая неправильная (некаталонская) сбалансированная строка начинается с , а оставшаяся строка имеет на один больше , чем , поэтому $c)$ $($ $)$

B_{n+1}-C_{n+1}=\sum _{i=0}^{n}{2i+1 \choose i}C_{n-i}

Также из определений следует:

B_{n+1}-C_{n+1}=2\sum _{i=0}^{n}B_{i}C_{n-i}-\sum _{i=0}^{n}C_{i}\,C_{n-i}=\sum _{i=0}^{n}(2B_{i}-C_{i})C_{n-i}.

Следовательно, поскольку это верно для всех $n$ ,

2B_{i}-C_{i}={\binom {2i+1}{i}}

C_{i}=2B_{i}-{\binom {2i+1}{i}}

C_{i}=2{\binom {2i}{i}}-{\binom {2i+1}{i}}

C_{i}={\frac {1}{i+1}}{\binom {2i}{i}}

Шестое доказательство

Это доказательство основано на интерпретации слов Дика каталонских чисел и использует лемму о циклах Дворецкого и Моцкина. ^[11]^[12]

Мы называем последовательность X и Y доминирующей , если, читая слева направо, число X всегда строго больше числа Y. Лемма о цикле ^[13] утверждает, что любая последовательность X и Y, где , имеет ровно доминирующие круговые сдвиги . Чтобы увидеть это, расположим заданную последовательность X и Y в круг. Повторное удаление пар XY оставляет ровно X. Каждый из этих X был началом доминирующего кругового сдвига до того, как что-либо было удалено. Например, рассмотрим . Эта последовательность является доминирующей, но ни один из ее круговых сдвигов , и не является. $m$ $n$ $m>n$ $m-n$ $m+n$ $m-n$ ${\mathit {XXYXY}}$ ${\mathit {XYXYX}}$ ${\mathit {YXYXX}}$ ${\mathit {XYXXY}}$ ${\mathit {YXXYX}}$

Строка является словом Дика из X и Y тогда и только тогда, когда добавление X к слову Дика дает доминирующую последовательность с X и Y, поэтому мы можем подсчитать первую, вместо того чтобы подсчитать вторую. В частности, когда , существует ровно один доминирующий циклический сдвиг. Существуют последовательности с ровно X и Y. Для каждого из них только один из циклических сдвигов является доминирующим. Следовательно, существуют различные последовательности X и Y, которые являются доминирующими, каждая из которых соответствует ровно одному слову Дика. $n$ $n$ $n+1$ $n$ $m=n+1$ $\textstyle {2n+1 \choose n}$ $n+1$ $n$ $2n+1$ $\textstyle {\frac {1}{2n+1}}{2n+1 \choose n}=C_{n}$ $n+1$ $n$

матрица Ганкеля

Матрица Ганкеля $n \times n,$ $элемент ($ $i$ $,$ $j$ $)$ которой является каталонским числом $C$ $i$ $+$ $j$ $-2,$ имеет определитель 1, независимо от значения $n$ . Например, для $n$ $= 4$ мы имеем

\det {\begin{bmatrix}1&1&2&5\\1&2&5&14\\2&5&14&42\\5&14&42&132\end{bmatrix}}=1.

Более того, если индексация «сдвинута» так, что запись $(i, j)$ заполнена каталонским числом $C i + j -1,$ то определитель все еще равен 1, независимо от значения $n$ . Например, для $n = 4$ мы имеем

\det {\begin{bmatrix}1&2&5&14\\2&5&14&42\\5&14&42&132\\14&42&132&429\end{bmatrix}}=1.

В совокупности эти два условия однозначно определяют каталонские числа.

Еще одной уникальной особенностью матрицы Каталана–Ганкеля является то, что подматрица $n \times n,$ начинающаяся с $2,$ имеет определитель $n + 1$ .

\det {\begin{bmatrix}2\end{bmatrix}}=2

\det {\begin{bmatrix}2&5\\5&14\end{bmatrix}}=3

\det {\begin{bmatrix}2&5&14\\5&14&42\\14&42&132\end{bmatrix}}=4

\det {\begin{bmatrix}2&5&14&42\\5&14&42&132\\14&42&132&429\\42&132&429&1430\end{bmatrix}}=5

и так далее.

История

Последовательность Каталана была описана в 1751 году Леонардом Эйлером , который интересовался количеством различных способов деления многоугольника на треугольники. Последовательность названа в честь Эжена Шарля Каталана , который обнаружил связь с выражениями в скобках во время своего исследования головоломки «Ханойские башни» . Трюк с подсчетом отражений (второе доказательство) для слов Дика был найден Дезире Андре в 1887 году.

Название «каталонские числа» произошло от Джона Риордана . ^[14]

В 1988 году выяснилось, что каталонская числовая последовательность использовалась в Китае монгольским математиком Минганту к 1730 году. ^[15]^[16] Именно тогда он начал писать свою книгу Ge Yuan Mi Lu Jie Fa [Быстрый метод получения точного отношения деления круга] , которая была завершена его учеником Чэнь Цзисинем в 1774 году, но опубликована шестьдесят лет спустя. Питер Дж. Ларкомб (1999) обрисовал некоторые черты работы Минганту, включая стимул Пьера Жарту, который привез три бесконечных ряда в Китай в начале 1700-х годов.

Например, Минг использовал каталонскую последовательность для выражения разложений рядов и в терминах . $\sin(2\alpha )$ $\sin(4\alpha )$ $\sin(\alpha )$

Обобщения

Числа Каталана можно интерпретировать как частный случай теоремы Бертрана о голосовании . В частности, это число способов для кандидата A с $n$ $+ 1$ голосами опередить кандидата B с $n$ голосами. $C_{n}$

Двухпараметрическая последовательность неотрицательных целых чисел является обобщением каталонских чисел. Они называются суперкаталонскими числами , по Айре Гессель . Их не следует путать с числами Шредера–Гиппарха , которые иногда также называют суперкаталонскими числами. ${\frac {(2m)!(2n)!}{(m+n)!m!n!}}$

Для это всего лишь два раза больше обычных каталонских чисел, а для числа имеют простое комбинаторное описание. Однако другие комбинаторные описания известны только ^[17] для и , ^[18] и это открытая проблема — найти общую комбинаторную интерпретацию. $m=1$ $m=n$ $m=2,3$ $4$

Сергей Фомин и Натан Рединг дали обобщенное число Каталана, связанное с любой конечной кристаллографической группой Коксетера , а именно число полностью коммутативных элементов группы; в терминах связанной корневой системы это число антицепей (или идеалов порядка) в частично упорядоченном множестве положительных корней. Классическое число Каталана соответствует корневой системе типа . Классическое рекуррентное соотношение обобщает: число Каталана диаграммы Коксетера равно сумме чисел Каталана всех ее максимальных собственных поддиаграмм. ^[19] $C_{n}$ $A_{n}$

Числа Каталана являются решением версии проблемы моментов Хаусдорфа . ^[20]

Каталонская k-кратная свертка

Каталонская $k$ -кратная свертка, где $k = m$ , имеет вид: ^[21]

\sum _{i_{1}+\cdots +i_{m}=n \atop i_{1},\ldots ,i_{m}\geq 0}C_{i_{1}}\cdots C_{i_{m}}={\begin{cases}{\dfrac {m(n+1)(n+2)\cdots (n+m/2-1)}{2(n+m/2+2)(n+m/2+3)\cdots (n+m)}}C_{n+m/2},&m{\text{ even,}}\\[5pt]{\dfrac {m(n+1)(n+2)\cdots (n+(m-1)/2)}{(n+(m+3)/2)(n+(m+3)/2+1)\cdots (n+m)}}C_{n+(m-1)/2},&m{\text{ odd.}}\end{cases}}

Смотрите также

Примечания

^ Коши, Томас; Салмасси, Мохаммад (2006). «Четность и простота каталонских чисел» (PDF) . The College Mathematics Journal . 37 (1): 52– 53. doi :10.2307/27646275. JSTOR 27646275.
^ Слоан, Н. Дж. А. (ред.). "Последовательность A000108 (каталонские числа)". Онлайновая энциклопедия целочисленных последовательностей . Фонд OEIS.
^ «Каталонское число».
^ Чой, Хаёнг; Йе, Ён-Нан; Ю, Сонгук (2020), «Последовательности чисел, подобные каталонским, и последовательности моментов Хаусдорфа», Дискретная математика , 343 (5): 111808, 11, arXiv : 1809.07523 , doi : 10.1016/j.disc.2019.111808, MR 4052255, S2CID 214165563 , Пример 3.1
^ Фэн, Ци; Бай-Ни, Го (2017), «Интегральные представления каталонских чисел и их приложения», Mathematics , 5 (3): 40, doi : 10.3390/math5030040,Теорема 1
^ Пути Дика
^ Стэнли стр. 221 пример (e)
^ Črepinšek, Matej; Mernik, Luka (2009). "Эффективное представление для решения задач, связанных с каталонскими числами" (PDF) . International Journal of Pure and Applied Mathematics . 56 (4): 589–604 .
^ А. де Сегнер, Enumeratio modorum, quibus figurae planae Rectilineae по диагоналям разделенных в треугольнике. Novi commentarii academiae scientiarum Petropolitanae 7 (1758/59) 203–209.
^ Рукавицка Йозеф (2011), Об обобщенных путях Дика, Электронный журнал комбинаторики онлайн
^ Дершовиц, Нахум; Закс, Шмуэль (1980), «Перечисления упорядоченных деревьев», Дискретная математика , 31 : 9–28 , doi :10.1016/0012-365x(80)90168-5, hdl : 2027/uiuo.ark:/13960/t3kw6z60d
^ Дворецкий, Арье; Моцкин, Теодор (1947), «Проблема размещений», Duke Mathematical Journal , 14 (2): 305–313 , doi :10.1215/s0012-7094-47-01423-3
^ Дершовиц, Нахум; Закс, Шмуэль (январь 1990 г.). «The Cycle Lemma and Some Applications» (PDF) . European Journal of Combinatorics . 11 (1): 35– 40. doi :10.1016/S0195-6698(13)80053-4.
^ Стэнли, Ричард П. (2021). «Перечислительная и алгебраическая комбинаторика в 1960-х и 1970-х годах». arXiv : 2105.07884 [math.HO].
^ Ларкомб, Питер Дж. «Открытие каталонских чисел китайцами в XVIII веке» (PDF) .
^ "Мин Анту, первый изобретатель каталонских чисел в мире". Архивировано из оригинала 2020-01-31 . Получено 2014-06-24 .
^ Чен, Синь; Ван, Джейн (2012). "Суперкаталонские числа S(m, m + s) для s ≤ 4". arXiv : 1208.4196 [math.CO].
^ Георгичук, Ирина; Ореловиц, Гидон (2020). «Суперкаталонские числа третьего и четвертого рода». arXiv : 2008.00133 [math.CO].
^ Сергей Фомин и Натан Рединг, «Корневые системы и обобщенные ассоциэдры», Геометрическая комбинаторика, IAS/Park City Math. Сер. 13 , Американское математическое общество , Провиденс, Род-Айленд, 2007, стр. 63–131. arXiv :math/0505518
^ Чой, Хаёнг; Йе, Ён-Нан; Ю, Сонгук (2020), «Последовательности чисел, подобные каталонским, и последовательности моментов Хаусдорфа», Дискретная математика , 343 (5): 111808, 11, arXiv : 1809.07523 , doi : 10.1016/j.disc.2019.111808, MR 4052255, S2CID 214165563
^ Боуман, Д.; Регев, Алон (2014). «Подсчет симметрии: классы разрезов выпуклого правильного многоугольника». Adv. Appl. Math . 56 : 35–55 . arXiv : 1209.6270 . doi : 10.1016/j.aam.2014.01.004 . S2CID 15430707.

Ссылки

Стэнли, Ричард П. (2015), Каталонские числа . Cambridge University Press, ISBN 978-1-107-42774-7 .
Конвей и Гай (1996) Книга чисел . Нью-Йорк: Copernicus, стр. 96–106.
Гарднер, Мартин (1988), Путешествия во времени и другие математические недоумения, Нью-Йорк: WH Freeman and Company, стр. 253–266 (гл. 20), Bibcode : 1988ttom.book.....G, ISBN 0-7167-1924-X
Коши, Томас (2008), Каталонские числа с приложениями, Oxford University Press, ISBN 978-0-19-533454-8
Коши, Томас и Чжэньгуан Гао (2011) «Некоторые свойства делимости каталонских чисел», Mathematical Gazette 95:96–102.
Larcombe, PJ (1999). «Китайское открытие каталонских чисел в XVIII веке» (PDF) . Mathematical Spectrum . 32 : 5–7 .
Стэнли, Ричард П. (1999), Перечислительная комбинаторика. Том 2, Cambridge Studies in Advanced Mathematics, том 62, Cambridge University Press , ISBN 978-0-521-56069-6, г-н 1676282
Эгесиоглу, Омер (2009), Оценка детерминанта Каталана–Ганкеля (PDF)
Георгичук, Ирина; Ореловиц, Гидон (2020), Суперкаталонские числа третьего и четвертого рода , arXiv : 2008.00133

Внешние ссылки

Стэнли, Ричард П. (1998), Каталонское дополнение к «Перечислительной комбинаторике», том 2 (PDF)
Вайсштейн, Эрик В. «Каталонское число». MathWorld .
Дэвис, Том: Каталонские числа. Еще больше примеров.
«Эквивалентность трех каталонских интерпретаций чисел» из проекта Wolfram Demonstrations Project [1]
Учебные материалы по теме «Разбиение связанных числовых треугольников» в Викиверситете

[1] Коши, Томас; Салмасси, Мохаммад (2006). «Четность и простота каталонских чисел» (PDF) . The College Mathematics Journal . 37 (1): 52– 53. doi :10.2307/27646275. JSTOR 27646275.

[2] Слоан, Н. Дж. А. (ред.). "Последовательность A000108 (каталонские числа)". Онлайновая энциклопедия целочисленных последовательностей . Фонд OEIS.

[3] «Каталонское число».

[4] Чой, Хаёнг; Йе, Ён-Нан; Ю, Сонгук (2020), «Последовательности чисел, подобные каталонским, и последовательности моментов Хаусдорфа», Дискретная математика , 343 (5): 111808, 11, arXiv : 1809.07523 , doi : 10.1016/j.disc.2019.111808, MR 4052255, S2CID 214165563 , Пример 3.1

[5] Фэн, Ци; Бай-Ни, Го (2017), «Интегральные представления каталонских чисел и их приложения», Mathematics , 5 (3): 40, doi : 10.3390/math5030040,Теорема 1

[6] Пути Дика

[7] Стэнли стр. 221 пример (e)

[8] Črepinšek, Matej; Mernik, Luka (2009). "Эффективное представление для решения задач, связанных с каталонскими числами" (PDF) . International Journal of Pure and Applied Mathematics . 56 (4): 589–604 .

[9] А. де Сегнер, Enumeratio modorum, quibus figurae planae Rectilineae по диагоналям разделенных в треугольнике. Novi commentarii academiae scientiarum Petropolitanae 7 (1758/59) 203–209.

[10] Рукавицка Йозеф (2011), Об обобщенных путях Дика, Электронный журнал комбинаторики онлайн

[11] Дершовиц, Нахум; Закс, Шмуэль (1980), «Перечисления упорядоченных деревьев», Дискретная математика , 31 : 9–28 , doi :10.1016/0012-365x(80)90168-5, hdl : 2027/uiuo.ark:/13960/t3kw6z60d

[12] Дворецкий, Арье; Моцкин, Теодор (1947), «Проблема размещений», Duke Mathematical Journal , 14 (2): 305–313 , doi :10.1215/s0012-7094-47-01423-3

[13] Дершовиц, Нахум; Закс, Шмуэль (январь 1990 г.). «The Cycle Lemma and Some Applications» (PDF) . European Journal of Combinatorics . 11 (1): 35– 40. doi :10.1016/S0195-6698(13)80053-4.

[14] Стэнли, Ричард П. (2021). «Перечислительная и алгебраическая комбинаторика в 1960-х и 1970-х годах». arXiv : 2105.07884 [math.HO].

[15] Ларкомб, Питер Дж. «Открытие каталонских чисел китайцами в XVIII веке» (PDF) .

[16] "Мин Анту, первый изобретатель каталонских чисел в мире". Архивировано из оригинала 2020-01-31 . Получено 2014-06-24 .

[Chen2012-17] Чен, Синь; Ван, Джейн (2012). "Суперкаталонские числа S(m, m + s) для s ≤ 4". arXiv : 1208.4196 [math.CO].

[18] Георгичук, Ирина; Ореловиц, Гидон (2020). «Суперкаталонские числа третьего и четвертого рода». arXiv : 2008.00133 [math.CO].

[19] Сергей Фомин и Натан Рединг, «Корневые системы и обобщенные ассоциэдры», Геометрическая комбинаторика, IAS/Park City Math. Сер. 13 , Американское математическое общество , Провиденс, Род-Айленд, 2007, стр. 63–131. arXiv :math/0505518

[20] Чой, Хаёнг; Йе, Ён-Нан; Ю, Сонгук (2020), «Последовательности чисел, подобные каталонским, и последовательности моментов Хаусдорфа», Дискретная математика , 343 (5): 111808, 11, arXiv : 1809.07523 , doi : 10.1016/j.disc.2019.111808, MR 4052255, S2CID 214165563

[21] Боуман, Д.; Регев, Алон (2014). «Подсчет симметрии: классы разрезов выпуклого правильного многоугольника». Adv. Appl. Math . 56 : 35–55 . arXiv : 1209.6270 . doi : 10.1016/j.aam.2014.01.004 . S2CID 15430707.