Распределение заусенцев
Тип заусенца XII
Функция плотности вероятности
Кумулятивная функция распределения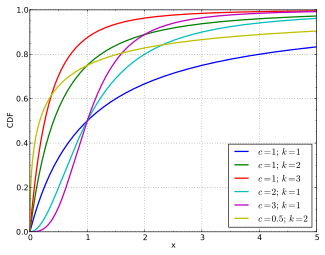
Параметры с > 0 {\displaystyle c>0\!}
к > 0 {\displaystyle к>0\!}
Поддерживать х > 0 {\displaystyle x>0\!}
PDF с к х с − 1 ( 1 + х с ) к + 1 {\displaystyle ck{\frac {x^{c-1}}{(1+x^{c})^{k+1}}}\!}
СДФ 1 − ( 1 + х с ) − к {\displaystyle 1-\left(1+x^{c}\right)^{-k}}
Квантиль λ ( 1 ( 1 − У ) 1 к − 1 ) 1 с {\displaystyle \lambda \left({\frac {1}{(1-U)^{\frac {1}{k}}}}-1\right)^{\frac {1}{c}}}
Иметь в виду μ 1 = к Б ⁡ ( к − 1 / с , 1 + 1 / с ) {\displaystyle \mu _{1}=k\operatorname {\mathrm {B}} (k-1/c,\,1+1/c)} где Β() — бета-функция
Медиана ( 2 1 к − 1 ) 1 с {\displaystyle \left(2^{\frac {1}{k}}-1\right)^{\frac {1}{c}}}
Режим ( с − 1 к с + 1 ) 1 с {\displaystyle \left({\frac {c-1}{kc+1}}\right)^{\frac {1}{c}}}
Дисперсия − μ 1 2 + μ 2 {\displaystyle -\mu _{1}^{2}+\mu _{2}}
Асимметрия 2 μ 1 3 − 3 μ 1 μ 2 + μ 3 ( − μ 1 2 + μ 2 ) 3 / 2 {\displaystyle {\frac {2\mu _{1}^{3}-3\mu _{1}\mu _{2}+\mu _{3}}{\left(-\mu _{1 }^{2}+\mu _{2}\right)^{3/2}}}}
Избыточный эксцесс − 3 μ 1 4 + 6 μ 1 2 μ 2 − 4 μ 1 μ 3 + μ 4 ( − μ 1 2 + μ 2 ) 2 − 3 {\displaystyle {\frac {-3\mu _{1}^{4}+6\mu _{1}^{2}\mu _{2}-4\mu _{1}\mu _{3 }+\mu _{4}}{\left(-\mu _{1}^{2}+\mu _{2}\right)^{2}}}-3} где моменты (см.) μ г = к Б ⁡ ( с к − г с , с + г с ) {\displaystyle \mu _{r}=k\operatorname {\mathrm {B} } \left({\frac {ck-r}{c}},\,{\frac {c+r}{c}}\right)}
CF = с ( − я т ) к с Г ( к ) ЧАС 1 , 2 2 , 1 [ ( − я т ) с | ( − к , 1 ) ( 0 , 1 ) , ( − к с , с ) ] , т ≠ 0 {\displaystyle ={\frac {c(-it)^{kc}}{\Gamma (k)}}H_{1,2}^{2,1}\!\left[(-it)^{c}\left|{\begin{matrix}(-k,1)\\(0,1),(-kc,c)\end{matrix}}\right.\right],t\neq 0}
= 1 , т = 0 {\displaystyle =1,t=0}
где — гамма-функция , а — H-функция Фокса . [1] Г {\displaystyle \Гамма} ЧАС {\displaystyle H}

В теории вероятностей , статистике и эконометрике распределение Берра типа XII или просто распределение Берра [2] представляет собой непрерывное распределение вероятностей для неотрицательной случайной величины . Оно также известно как распределение Сингха–Маддалы [3] и является одним из ряда различных распределений, иногда называемых «обобщенным лог-логистическим распределением ».

Определения

Функция плотности вероятности

Распределение Берра (тип XII) имеет функцию плотности вероятности : [4] [5]

ф ( х ; с , к ) = с к х с − 1 ( 1 + х с ) к + 1 ф ( х ; с , к , λ ) = с к λ ( х λ ) с − 1 [ 1 + ( х λ ) с ] − к − 1 {\displaystyle {\begin{align}f(x;c,k)&=ck{\frac {x^{c-1}}{(1+x^{c})^{k+1}}}\\[6pt]f(x;c,k,\lambda )&={\frac {ck}{\lambda }}\left({\frac {x}{\lambda }}\right)^{c-1}\left[1+\left({\frac {x}{\lambda }}\right)^{c}\right]^{-k-1}\end{align}}}

Параметр масштабирует базовую переменную и является положительным действительным числом. λ {\displaystyle \лямбда}

Кумулятивная функция распределения

Кумулятивная функция распределения имеет вид:

Ф ( х ; с , к ) = 1 − ( 1 + х с ) − к {\displaystyle F(x;c,k)=1-\left(1+x^{c}\right)^{-k}}
Ф ( х ; с , к , λ ) = 1 − [ 1 + ( х λ ) с ] − к {\displaystyle F(x;c,k,\lambda )=1-\left[1+\left({\frac {x}{\lambda }}\right)^{c}\right]^{-k}}

Приложения

Чаще всего он используется для моделирования дохода домохозяйства , см., например: Доход домохозяйства в США и сравните с пурпурным графиком справа.

Генерация случайных величин

Дана случайная величина, взятая из равномерного распределения в интервале , случайная величина У {\displaystyle U} ( 0 , 1 ) {\displaystyle \left(0,1\right)}

Х = λ ( 1 1 − У к − 1 ) 1 / с {\displaystyle X=\lambda \left({\frac {1}{\sqrt[{k}]{1-U}}}-1\right)^{1/c}}

имеет распределение типа Берра XII с параметрами , и . Это следует из обратной кумулятивной функции распределения, приведенной выше. с {\displaystyle с} к {\displaystyle к} λ {\displaystyle \лямбда}

  • Распределение типа XII Берра является элементом системы непрерывных распределений, введенной Ирвингом У. Берром (1942), которая включает 12 распределений. [8]
  • Распределение Дагума , также известное как обратное распределение Берра, представляет собой распределение 1 / X , где X имеет распределение Берра

Ссылки

  1. ^ Nadarajah, S.; Pogány, TK; Saxena, RK (2012). «О характеристической функции для распределений Берра». Статистика . 46 (3): 419–428. doi :10.1080/02331888.2010.513442. S2CID  120848446.
  2. ^ Burr, IW (1942). "Функции кумулятивной частоты". Annals of Mathematical Statistics . 13 (2): 215–232. doi : 10.1214/aoms/1177731607 . JSTOR  2235756.
  3. ^ Сингх, С.; Маддала, Г. (1976). «Функция распределения доходов по размеру». Econometrica . 44 (5): 963–970. doi :10.2307/1911538. JSTOR  1911538.
  4. ^ Маддала, GS (1996) [1983]. Ограниченно-зависимые и качественные переменные в эконометрике . Cambridge University Press. ISBN 0-521-33825-5.
  5. ^ Тадикамалла, Панду Р. (1980), «Взгляд на Burr и связанные с ним распределения», International Statistical Review , 48 (3): 337–344, doi : 10.2307/1402945, JSTOR  1402945
  6. ^ C. Kleiber и S. Kotz (2003). Статистические распределения размеров в экономике и актуарных науках . Нью-Йорк: Wiley.См. разделы 7.3 «Распределение Чамперноуна» и 6.4.1 «Распределение Фиска».
  7. ^ Чамперноун, Д. Г. (1952). «Градуировка распределения доходов». Econometrica . 20 (4): 591–614. doi :10.2307/1907644. JSTOR  1907644.
  8. ^ См. Клейбер и Котц (2003), Таблица 2.4, стр. 51, «Распределения Берра».

Дальнейшее чтение

  • Родригес, Р. Н. (1977). «Руководство по распределениям типа XII Берра». Biometrika . 64 (1): 129–134. doi :10.1093/biomet/64.1.129.
  • Джон (16.02.2023). "Другие дистрибутивы Burr". www.johndcook.com .
Взято с "https://en.wikipedia.org/w/index.php?title=Burr_distribution&oldid=1224329430"