Алгоритм Брандеса

Алгоритм Брандеса

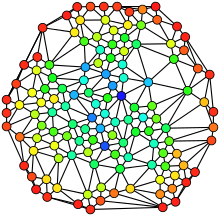Неориентированный граф , раскрашенный в зависимости от центральности каждой вершины по промежуточному признаку от наименьшего (красный) до наибольшего (синий).
Сорт	Теория сети центральности
Структура данных	Связный граф
Худший вариант производительности	${\displaystyle O(|V||E|)}$(невзвешенный) (взвешенный) ${\displaystyle O(|V||E|+|V|^{2}\log |V|)}$
Наихудшая сложность пространства	${\displaystyle O(|V|+|E|)}$

В теории сетей алгоритм Брандеса — это алгоритм для вычисления центральности по промежуточности вершин в графе . Алгоритм был впервые опубликован в 2001 году Ульриком Брандесом . ^[1] Центральность по промежуточности, наряду с другими мерами центральности , является важной мерой во многих реальных сетях, таких как социальные сети и компьютерные сети . ^{[2] [3] [4]}

Существует несколько метрик для центральности узла, одна из которых — промежуточная центральность . ^[5] Для узла в связном графе промежуточная центральность определяется как: ^{[6] [7]}${\displaystyle v}$

${\displaystyle C_{B}(v)=\sum _{s\in V} \sum _{t\in V}{\frac {\sigma _{st}(v)}{\sigma _{st} }}}$

где — общее число кратчайших путей от узла до узла , а — число этих путей, проходящих через . Для невзвешенного графа длина пути считается числом содержащихся в нем ребер.${\displaystyle \сигма _{ст}}$${\displaystyle с}$${\displaystyle т}$${\displaystyle \sigma _{st}(v)}$${\displaystyle v}$

По соглашению, всякий раз , когда , поскольку единственный путь — это пустой путь. Также, если это либо или , поскольку кратчайшие пути не проходят через свои конечные точки.${\displaystyle \сигма _{ст}=1}$${\displaystyle с=т}$${\displaystyle \sigma _{st}(v)=0}$${\displaystyle v}$${\displaystyle с}$${\displaystyle т}$

Количество

${\displaystyle \delta _{st}(v)={\frac {\sigma _{st}(v)}{\sigma _{st}}}}$

известна как парная зависимость от и представляет собой долю кратчайших – путей , проходящих через . Центральность по промежуточности – это просто сумма парных зависимостей по всем парам. Помимо парной зависимости, также полезно определить ( отдельную) зависимость от относительно конкретной вершины :${\displaystyle ст}$${\displaystyle v}$${\displaystyle с}$${\displaystyle т}$${\displaystyle v}$${\displaystyle v}$${\displaystyle с}$

${\displaystyle \delta _{s}(v)=\sum _{t\in V}\delta _{st}(v)}$,

с помощью которого мы можем получить краткую формулировку

${\displaystyle C_{B}(v)=\sum _{s\in V}\delta _{s}(v)}$.

Алгоритм Брандеса вычисляет центральность посредничества всех узлов в графе. Для каждой вершины есть два этапа.${\displaystyle с}$

Количество кратчайших путей между и каждой вершиной вычисляется с помощью поиска в ширину . Поиск в ширину начинается с , и записывается кратчайшее расстояние каждой вершины от , разделяя граф на дискретные слои. Кроме того, каждая вершина отслеживает набор вершин, которые в предыдущем слое указывают на нее, . Описанный в нотации set-builder , он может быть записан как:${\displaystyle \сигма _{св}}$${\displaystyle с}$${\displaystyle v}$${\displaystyle с}$${\displaystyle d(v)}$${\displaystyle с}$${\displaystyle v}$${\displaystyle p(v)}$

${\displaystyle p(v)=\{u\in V\mid (u,v)\in E\land d(u)+1=d(v)\}}$.

Это приводит к простой итеративной формуле :${\displaystyle \sigma _{sv}}$

${\displaystyle \sigma _{sv}=\sum _{u\in p(v)}\sigma _{su}}$,

что по сути утверждает, что если находится на глубине , то любой кратчайший путь на глубине , расширенный одним ребром до , становится кратчайшим путем к .${\displaystyle v}$${\displaystyle d(v)}$${\displaystyle d(v)-1}$${\displaystyle v}$${\displaystyle v}$

Брандес доказал следующую рекурсивную формулу для вершинных зависимостей: ^[1]

${\displaystyle \delta _{s}(u)=\sum _{v\mid u\in p(v)}{\frac {\sigma _{su}}{\sigma _{sv}}}\cdot (1+\delta _{s}(v))}$,

где сумма берется по всем вершинам , которые находятся на одно ребро дальше от . Эта лемма устраняет необходимость явно суммировать все парные зависимости. Используя эту формулу, единственная зависимость от вершины на глубине определяется слоем на глубине . Более того, порядок суммирования не имеет значения, что позволяет использовать подход снизу вверх, начиная с самого глубокого слоя.${\displaystyle v}$${\displaystyle s}$${\displaystyle u}$${\displaystyle s}$${\displaystyle u}$${\displaystyle d(u)}$${\displaystyle d(u)+1}$

Оказывается, зависимости от всех других вершин можно вычислить со временем. Во время поиска в ширину порядок посещения вершин регистрируется в структуре данных стека . Затем шаг обратного распространения многократно выталкивает вершины, которые естественным образом сортируются по расстоянию от , по убыванию.${\displaystyle s}$${\displaystyle u}$${\displaystyle O(|E|)}$${\displaystyle s}$

Для каждого вытолкнутого узла мы перебираем его предшественников : добавляется вклад в , то есть,${\displaystyle v}$${\displaystyle u\in p(v)}$${\displaystyle v}$${\displaystyle \delta _{s}(u)}$

${\displaystyle {\frac {\sigma _{su}}{\sigma _{sv}}}\cdot (1+\delta _{s}(v))}$.

Важно то, что каждый слой полностью распространяет свои зависимости, прежде чем перейти к слою с меньшей глубиной, из-за природы поиска в ширину. Как только распространение достигает обратно , каждая вершина теперь содержит . Их можно просто добавить к , поскольку${\displaystyle s}$${\displaystyle v}$${\displaystyle \delta _{s}(v)}$${\displaystyle C_{B}(v)}$

${\displaystyle C_{B}(v)=\sum _{s\in V}\delta _{s}(v)}$.

После итераций кратчайшего пути из одного источника и обратного распространения каждая содержит центральность по промежуточности для .${\displaystyle |V|}$${\displaystyle C_{B}(v)}$${\displaystyle v}$

Следующий псевдокод иллюстрирует алгоритм Брандеса на невзвешенном ориентированном графе. ^[8]

Алгоритм Брандеса ( Graph ) для  каждого  u  в  Graph.Vertices  делают CB[ u ] ← 0 для каждого  s  в  Graph.Vertices  сделать  для каждого  v  в  Graph.Vertices  сделать δ[ v ] ← 0 // Одиночная зависимость s от v prev[ v ] ← пустой список // Непосредственные предшественники v во время BFS σ[ v ] ← 0 // Количество кратчайших путей от s до v (s подразумевается) dist[ v ] ← null // Изначально пути неизвестны, σ[ s ] ← 1 // за исключением начальной вершины расст[ с ] ← 0 Q ← очередь, содержащая только s // Поиск в ширину S ← пустой стек // Запись порядка посещения вершин // Кратчайшие пути из одного источника пока  Q не пусто do  u ← Q .dequeue() S .push( u ) для каждого  v  в  Graph.Neighbours [ u ] do  if dist[ v ] = null  then dist[ v ] ← dist[ u ] + 1 Q .enqueue( v ) if dist[ v ] = dist[ u ] + 1 then σ[ v ] ← σ[ v ] + σ[ u ] prev[ v ].append( u ) // Обратное распространение зависимостей пока  S не пусто do  v ← S .pop() для каждого  u  в prev[ v ] выполнить δ[ u ] ← δ[ u ] + σ[ u ] / σ[ v ] * (1 + δ[ v ]) если  u ≠ s  , то CB[ v ] ← CB[ v ] + δ[ v ] // Уменьшено вдвое для неориентированных графов возврат CB

Время работы алгоритма выражается через количество вершин и количество ребер .${\displaystyle |V|}$${\displaystyle |E|}$

Для каждой вершины мы запускаем поиск в ширину, что занимает время. Поскольку граф связный, компонент включает в себя термин, поскольку число ребер не менее .${\displaystyle s}$${\displaystyle O(|V|+|E|)}$${\displaystyle |E|}$${\displaystyle |V|}$${\displaystyle |V|-1}$

На этапе обратного распространения каждая вершина выталкивается из стека, а ее предшественники перебираются. Однако, поскольку каждая запись предшественника соответствует ребру в графе, этот этап также ограничен .${\displaystyle O(|E|)}$

Общее время работы алгоритма, таким образом, составляет , улучшение по сравнению с временными ограничениями, достигнутыми предыдущими алгоритмами. ^[1] Кроме того, алгоритм Брандеса улучшает пространственную сложность наивных алгоритмов, которые обычно требуют пространства. Алгоритм Брандеса хранит только большинство предшественников вместе с данными для каждой вершины, что делает его дополнительную пространственную сложность${\displaystyle O(|V||E|)}$${\displaystyle O(|V|^{3})}$${\displaystyle O(|V|^{2})}$${\displaystyle |E|}$${\displaystyle O(|V|+|E|)}$

Алгоритм может быть обобщен на взвешенные графы с использованием алгоритма Дейкстры вместо поиска в ширину. При работе с неориентированными графами центральность промежуточности может быть разделена на 2, чтобы избежать двойного подсчета обратного аналога каждого пути. Существуют также варианты для вычисления различных мер центральности, включая промежуточность с путями наибольшей длины , промежуточность ребер , промежуточность нагрузки и промежуточность напряжения . ^[8]${\displaystyle k}$