Диаграмма ящика
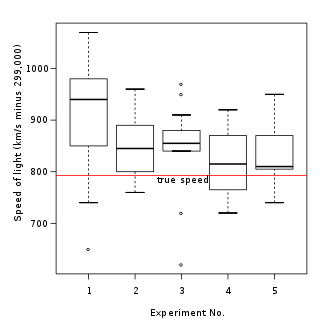
В описательной статистике ящичная диаграмма или коробчатая диаграмма — это метод графической демонстрации локальности, распространения и асимметрии групп числовых данных через их квартили . [1] В дополнение к ящику на ящичной диаграмме могут быть линии (которые называются усами ), выходящие из ящика, указывающие на изменчивость за пределами верхнего и нижнего квартилей, таким образом, график также называется диаграммой ящика и усов и диаграммой ящика и усов . Выбросы , которые значительно отличаются от остальной части набора данных [2], могут быть нанесены на график как отдельные точки за пределами усов на ящичной диаграмме. Ящичные диаграммы являются непараметрическими : они отображают изменчивость в выборках статистической совокупности без каких-либо предположений о базовом статистическом распределении [3] (хотя ящичная диаграмма Тьюки предполагает симметрию для усов и нормальность для их длины). Интервалы в каждом подразделе диаграммы ящиков указывают на степень дисперсии (разброса) и асимметрии данных, которые обычно описываются с помощью пятичислового резюме . Кроме того, диаграмма ящиков позволяет визуально оценить различные L-оценки , в частности, межквартильный размах , середину , диапазон , средний размах и тримедиа . Диаграммы ящиков можно рисовать как горизонтально, так и вертикально.
История
Метод диапазона-линии был впервые представлен Мэри Элеанор Спир в ее книге «Построение диаграмм статистики» в 1952 году [4] и затем в ее книге «Практические методы построения диаграмм» в 1969 году. [5] Диаграмма «ящик с усами» была впервые представлена в 1970 году Джоном Тьюки , который позже опубликовал работу по этой теме в своей книге «Исследовательский анализ данных» в 1977 году. [6]
Элементы


Ящичная диаграмма — это стандартизированный способ отображения набора данных на основе сводки из пяти чисел : минимума, максимума, выборочной медианы, а также первого и третьего квартилей.
- Минимум ( Q 0 или 0-й процентиль ) : самая низкая точка данных в наборе данных, исключая любые выбросы.
- Максимум ( Q 4 или 100-й процентиль) : наивысшая точка данных в наборе данных, исключая любые выбросы.
- Медиана ( Q 2 или 50-й процентиль) : среднее значение в наборе данных
- Первый квартиль ( Q 1 или 25-й процентиль) : также известный как нижний квартиль q n (0,25), это медиана нижней половины набора данных.
- Третий квартиль ( Q 3 или 75-й процентиль) : также известный как верхний квартиль q n (0,75), это медиана верхней половины набора данных. [7]
Помимо минимальных и максимальных значений, используемых для построения диаграммы размаха, еще одним важным элементом, который также можно использовать для получения диаграммы размаха, является межквартильный размах (IQR), как обозначено ниже:
- Межквартильный размах (IQR) : расстояние между верхним и нижним квартилями
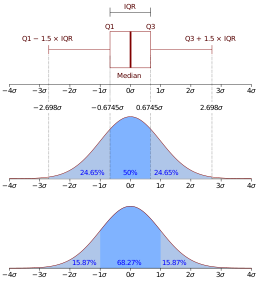
Ящичная диаграмма обычно состоит из двух частей: ящика и набора усов, как показано на рисунке 2.
Коробка
Ящик нарисован от Q 1 до Q 3 с горизонтальной линией внутри, обозначающей медиану. Некоторые ящики включают дополнительный символ, представляющий среднее значение данных. [8] [9]
Усы
Усы должны заканчиваться в точке наблюдаемых данных, но могут быть определены различными способами. В самом прямолинейном методе граница нижних усов является минимальным значением набора данных, а граница верхних усов является максимальным значением набора данных. Из-за этой изменчивости уместно описать соглашение, которое используется для усов и выбросов, в заголовке диаграммы ящиков.
Другой популярный выбор для границ усов основан на значении 1,5 IQR. Сверху от верхнего квартиля ( Q 3 ) отмеряется расстояние в 1,5 раза IQR и усы рисуются вверх до самой большой наблюдаемой точки данных из набора данных, который попадает в это расстояние. Аналогично, расстояние в 1,5 раза IQR отмеряется ниже нижнего квартиля ( Q 1 ) и усы рисуются вниз до самой низкой наблюдаемой точки данных из набора данных, который попадает в это расстояние. Поскольку усы должны заканчиваться в наблюдаемой точке данных, длины усов могут выглядеть неравными, даже несмотря на то, что 1,5 IQR одинаков для обеих сторон. Все другие наблюдаемые точки данных за пределами границы усов отображаются как выбросы . [10] Выбросы могут быть отображены на коробчатой диаграмме в виде точки, маленького круга, звезды и т. д. (см. пример ниже).
Существуют и другие представления, в которых усы могут обозначать несколько других вещей, например:
- Одно стандартное отклонение выше и ниже среднего значения набора данных
- 9-й процентиль и 91-й процентиль набора данных
- 2-й процентиль и 98-й процентиль набора данных
Редко, ящик-плот может быть построен без усов. Это может быть уместно для конфиденциальной информации, чтобы избежать усов (и выбросов), раскрывающих фактические наблюдаемые значения. [11]
Необычные процентили 2%, 9%, 91%, 98% иногда используются для штриховки усов и концов усов, чтобы изобразить сводку из семи чисел . Если данные распределены нормально , местоположения семи отметок на диаграмме ящиков будут равномерно распределены. На некоторых диаграммах ящиков штриховка помещается перед концом каждого уса.
Вариации
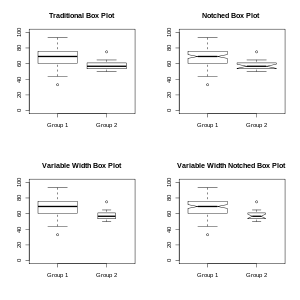
С тех пор как математик Джон У. Тьюки в 1969 году впервые популяризировал этот тип визуального отображения данных, было разработано несколько вариаций классической диаграммы ящиков, и две наиболее часто встречающиеся вариации — это диаграммы ящиков переменной ширины и диаграммы ящиков с выемками, показанные на рисунке 4.
Диаграммы ящиков переменной ширины иллюстрируют размер каждой группы, данные которой отображаются, делая ширину ящика пропорциональной размеру группы. Популярное соглашение заключается в том, чтобы сделать ширину ящика пропорциональной квадратному корню размера группы. [12]
В диаграммах с вырезами применяется «выемка» или сужение ящика вокруг медианы. Выемки полезны для приблизительного указания значимости разницы медиан; если выемки двух ящиков не перекрываются, это будет свидетельством статистически значимой разницы между медианами. [12] Высота выемок пропорциональна межквартильному размаху (IQR) выборки и обратно пропорциональна квадратному корню размера выборки. Однако существует неопределенность относительно наиболее подходящего множителя (так как он может варьироваться в зависимости от сходства дисперсий выборок). [12] Ширина выемки выбирается произвольно, чтобы быть визуально приятной, и должна быть одинаковой среди всех диаграмм с вырезами, отображаемых на одной странице.
Одним из соглашений для получения границ этих выемок является использование расстояния около медианы. [13]
Скорректированные диаграммы ящиков предназначены для описания асимметричных распределений и опираются на статистику асимметрии medcouple . [14] Для значения medcouple MC длины верхних и нижних усов на диаграмме ящиков соответственно определяются следующим образом:
Для симметричного распределения данных средняя пара будет равна нулю, и это сводит скорректированную диаграмму ящиков к диаграмме Тьюки с одинаковой длиной усов для обоих усов.
Другие виды диаграмм типа «ящик с усами» , такие как диаграммы скрипки и диаграммы фасоли, могут показать разницу между одномодальными и многомодальными распределениями, которую невозможно наблюдать из исходной классической диаграммы типа «ящик с усами». [6]
Примеры
Пример без выбросов
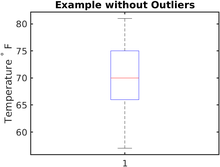
Ряд почасовых температур измерялся в течение дня в градусах Фаренгейта. Зарегистрированные значения перечислены в следующем порядке (°F): 57, 57, 57, 58, 63, 66, 66, 67, 67, 68, 69, 70, 70, 70, 70, 72, 73, 75, 75, 76, 76, 78, 79, 81.
Диаграмму размаха набора данных можно построить, сначала вычислив пять соответствующих значений этого набора данных: минимум, максимум, медиану ( Q2 ) , первый квартиль ( Q1 ) и третий квартиль ( Q3 ).
Минимум — наименьшее число в наборе данных. В этом случае минимальная зафиксированная дневная температура составляет 57°F.
Максимум — это наибольшее число в наборе данных. В этом случае максимальная зафиксированная дневная температура составляет 81°F.
Медиана — это «среднее» число упорядоченного набора данных. Это означает, что ровно 50% элементов находятся ниже медианы и 50% элементов больше медианы. Медиана этого упорядоченного набора данных составляет 70°F.
Значение первого квартиля ( Q 1 или 25-й процентиль) — это число, которое отмечает одну четверть упорядоченного набора данных. Другими словами, ровно 25% элементов меньше первого квартиля и ровно 75% элементов больше его. Значение первого квартиля можно легко определить, найдя «среднее» число между минимумом и медианой. Для почасовых температур «среднее» число между 57°F и 70°F составляет 66°F.
Значение третьего квартиля ( Q 3 или 75-й процентиль) — это число, которое отмечает три четверти упорядоченного набора данных. Другими словами, ровно 75% элементов меньше третьего квартиля и 25% элементов больше его. Значение третьего квартиля можно легко получить, найдя «среднее» число между медианой и максимумом. Для почасовых температур «среднее» число между 70°F и 81°F составляет 75°F.
Межквартильный размах, или IQR, можно рассчитать, вычитая значение первого квартиля ( Q 1 ) из значения третьего квартиля ( Q 3 ):
Следовательно,
1,5 IQR выше третьего квартиля составляет:
1,5 IQR ниже первого квартиля составляет:
Верхняя граница усов коробчатой диаграммы — это наибольшее значение данных, которое находится в пределах 1,5 IQR выше третьего квартиля. Здесь 1,5 IQR выше третьего квартиля составляет 88,5°F, а максимум — 81°F. Таким образом, верхний ус нарисован на значении максимума, которое составляет 81°F.
Аналогично, нижняя граница усов диаграммы ящиков — это наименьшее значение данных, которое находится в пределах 1,5 IQR ниже первого квартиля. Здесь 1,5 IQR ниже первого квартиля составляет 52,5°F, а минимум — 57°F. Таким образом, нижний ус нарисован на значении минимума, которое составляет 57°F.
Пример с выбросами

Выше приведен пример без выбросов. Ниже приведен пример для создания ящика с выбросами:
Упорядоченный набор зарегистрированных температур (°F): 52, 57, 57, 58, 63, 66, 66, 67, 67, 68, 69, 70, 70, 70, 70, 72, 73, 75, 75, 76, 76, 78, 79, 89.
В этом примере изменены только первое и последнее число. Медиана, третий квартиль и первый квартиль остаются прежними.
В этом случае максимальное значение в этом наборе данных составляет 89°F, а 1,5 IQR выше третьего квартиля составляет 88,5°F. Максимум больше, чем 1,5 IQR плюс третий квартиль, поэтому максимум является выбросом. Поэтому верхний ус нарисован на наибольшем значении, меньшем, чем 1,5 IQR выше третьего квартиля, что составляет 79°F.
Аналогично, минимальное значение в этом наборе данных составляет 52°F, а 1,5 IQR ниже первого квартиля составляет 52,5°F. Минимум меньше, чем 1,5 IQR минус первый квартиль, поэтому минимум также является выбросом. Поэтому нижний ус нарисован на наименьшем значении, большем, чем 1,5 IQR ниже первого квартиля, что составляет 57°F.
В случае больших наборов данных
Дополнительный пример получения диаграммы размаха из набора данных, содержащего большое количество точек данных:
Общее уравнение для вычисления эмпирических квантилей
- Здесь обозначается общий порядок точек данных (т.е. если , то )
Используя приведенный выше пример с 24 точками данных ( n = 24), можно рассчитать медиану, первый и третий квартиль математически или визуально.
Медиана :
Первый квартиль :
Третий квартиль :
Визуализация
Хотя диаграммы ящиков могут показаться более примитивными, чем гистограммы или оценки плотности ядра , у них есть ряд преимуществ. Во-первых, диаграмма ящиков позволяет статистикам проводить быструю графическую проверку одного или нескольких наборов данных. Диаграммы ящиков также занимают меньше места и поэтому особенно полезны для сравнения распределений между несколькими группами или наборами данных параллельно (см. пример на рисунке 1). Наконец, общая структура гистограмм и оценки плотности ядра может сильно зависеть от выбора количества и ширины методов бинов и выбора полосы пропускания соответственно.
Хотя статистическое распределение рассматривается чаще, чем диаграмма размаха, может быть полезно сравнить диаграмму размаха с функцией плотности вероятности (теоретической гистограммой) для нормального распределения N(0, σ2 ) и непосредственно наблюдать их характеристики (как показано на рисунке 7).

Смотрите также
- Багплот
- Контурная диаграмма
- График японских свечей
- Визуализация данных и информации
- Исследовательский анализ данных
- Веерная диаграмма
- Резюме из пяти чисел
- Функциональная диаграмма ящиков
- Резюме из семи чисел
- Сина участок
- Сюжет для скрипки
Ссылки
- ^ C., Dutoit, SH (2012). Графический анализ разведочных данных. Springer. ISBN 978-1-4612-9371-2. OCLC 1019645745.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ^ Граббс, Фрэнк Э. (февраль 1969 г.). «Процедуры обнаружения выпадающих наблюдений в образцах». Технометрика . 11 (1): 1–21. doi :10.1080/00401706.1969.10490657. ISSN 0040-1706.
- ^ Ричард., Бодди (2009). Статистические методы на практике: для ученых и технологов. John Wiley & Sons. ISBN 978-0-470-74664-6. OCLC 940679163.
- ^ Спир, Мэри Элеанор (2024). Статистика диаграмм . McGraw Hill. стр. 166.
- ^ Спир, Мэри Элеанор. (1969). Практические методы построения диаграмм . Нью-Йорк: McGraw-Hill. ISBN 0070600104. OCLC 924909765.
- ^ ab Wickham, Hadley; Stryjewski, Lisa. "40 years of boxplots" (PDF) . Получено 24 декабря 2020 г.
- ^ Холмс, Александр; Илловски, Барбара; Дин, Сьюзан (31 марта 2015 г.). «Введение в бизнес-статистику». OpenStax . Архивировано из оригинала 27 июля 2020 г. Получено 29 апреля 2020 г.
- ^ Фригге, Майкл; Хоглин, Дэвид К.; Иглевич, Борис (февраль 1989 г.). «Некоторые реализации ящика-диаграммы». The American Statistician . 43 (1): 50–54. doi :10.2307/2685173. JSTOR 2685173.
- ^ Мармолехо-Рамос, Ф.; Тиан, С. (2010). «Смещающаяся диаграмма типа «ящик с ящиками». Диаграмма типа «ящик с ящиками», основанная на существенных сводных статистических данных вокруг среднего значения». Международный журнал психологических исследований . 3 (1): 37–46. doi : 10.21500/20112084.823 . hdl : 10819/6492 .
- ^ Деккинг, Ф. М. (2005). Современное введение в теорию вероятностей и статистику . Springer. С. 234–238. ISBN 1-85233-896-2.
- ^ Деррик, Бен; Грин, Элизабет; Ричи, Феликс; Уайт, Пол (сентябрь 2022 г.). «Риск раскрытия при представлении общеупотребительной одномерной статистики». Конфиденциальность в статистических базах данных . Конспект лекций по информатике. Том 13463. С. 119–129. doi :10.1007/978-3-031-13945-1_9. ISBN 978-3-031-13944-4.
- ^ abc Макгилл, Роберт; Тьюки, Джон У.; Ларсен, Уэйн А. (февраль 1978 г.). «Вариации диаграмм ящиков». The American Statistician . 32 (1): 12–16. doi :10.2307/2683468. JSTOR 2683468.
- ^ "R: Box Plot Statistics". Руководство по R. Получено 26 июня 2011 г.
- ^ Hubert, M. ; Vandervieren, E. (2008). «Скорректированная диаграмма ящиков для асимметричного распределения». Computational Statistics and Data Analysis . 52 (12): 5186–5201. CiteSeerX 10.1.1.90.9812 . doi :10.1016/j.csda.2007.11.008.
Дальнейшее чтение
- Tukey, John W. (1977). Исследовательский анализ данных . Addison-Wesley . ISBN 9780201076165.
- Бенджамини, И. (1988). «Открывая ящик диаграммы». Американский статистик . 42 (4): 257–262. doi :10.2307/2685133. JSTOR 2685133.
- Rousseeuw, PJ ; Ruts, I.; Tukey, JW (1999). «The Bagplot: A Bivariate Boxplot». The American Statistician . 53 (4): 382–387. doi :10.2307/2686061. JSTOR 2686061.
Внешние ссылки
- Beeswarm Boxplot — наложение ленточной диаграммы с дрожанием частоты поверх ящичной диаграммы









![{\displaystyle {\text{с }}k=[p(n+1)]{\text{ и }}\alpha =p(n+1)-k}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c7fe0c9d05a9554dfbbd8dee8a39f0d779c1d39)






