Проблема укладки блоков

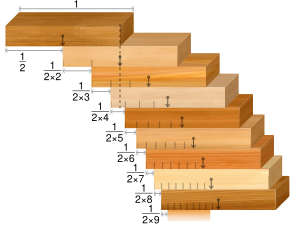
В статике задача об укладке блоков (иногда известная как «Падающая башня Лира» (Джонсон, 1955), а также задача об укладке книг или под рядом других похожих терминов) — головоломка, связанная с укладкой блоков на краю стола.

Задача на укладку блоков представляет собой следующую головоломку:

Разместите одинаковые жесткие прямоугольные блоки в устойчивой стопке на краю стола таким образом, чтобы максимально увеличить выступ.${\displaystyle N}$

Патерсон и др. (2007) приводят длинный список ссылок по этой проблеме, восходящий к текстам по механике середины XIX века.

Проблема одинарной ширины подразумевает наличие только одного блока на любом заданном уровне. В идеальном случае идеально прямоугольных блоков решение проблемы одинарной ширины заключается в том, что максимальный выступ задается как произведение ширины блока. Эта сумма составляет половину соответствующей частичной суммы гармонического ряда . Поскольку гармонический ряд расходится, максимальный выступ стремится к бесконечности по мере увеличения, что означает, что можно достичь любого произвольно большого выступа с достаточным количеством блоков.${\textstyle \sum _{i=1}^{N}{\frac {1}{2i}}}$ ${\displaystyle N}$

Количество блоков, необходимых для достижения по крайней мере длины блоков за пределами края таблицы, составляет 4, 31, 227, 1674, 12367, 91380, ... (последовательность A014537 в OEIS ). ^[1]${\displaystyle N}$

Многоширокие стопки с использованием противовеса могут давать большие выступы, чем стопка с одной шириной. Даже для трех блоков, укладка двух противовесных блоков поверх другого блока может дать выступ в 1, тогда как выступ в простом идеальном случае составляет максимум ⁠11/12⁠ . Как показали Патерсон и др. (2007), асимптотически максимальный выступ, который может быть достигнут с помощью многоширинных штабелей, пропорционален кубическому корню из числа блоков, в отличие от случая одинарной ширины, в котором выступ пропорционален логарифму числа блоков. Однако было показано, что в действительности это невозможно, и число блоков, которые мы можем переместить вправо из-за напряжения блока, не превышает заданного числа. Например, для специального кирпича с h =0,20 м , модуль Юнга E =3000 МПа и плотность ρ =1,8 × 10 ³  кг/м ³ и предельное напряжение сжатия3 МПа , приблизительное значение N будет равно 853, а максимальная высота башни станет170 м . ^[2]

Вышеприведенная формула для максимального свеса блоков, каждый с длиной и массой , сложенных по одному на уровне, может быть доказана методом индукции , рассматривая крутящие моменты на блоках относительно края стола, над которым они нависают. Блоки могут быть смоделированы как точечные массы, расположенные в центре каждого блока, предполагая равномерную плотность массы. В базовом случае ( ) центр масс блока лежит над краем стола, что означает свес . Для блоков центр масс системы -блоков должен лежать над краем стола, а центр масс верхних блоков должен лежать над краем первого для статического равновесия. ^[3] Если th-й блок нависает над th на , а свес первого равен , ^[4]${\displaystyle n}$${\displaystyle л}$${\displaystyle м}$${\displaystyle n=1}$${\displaystyle л/2}$${\displaystyle к}$${\displaystyle к}$${\displaystyle к-1}$${\displaystyle к}$${\displaystyle (к-1)}$${\displaystyle л/2}$${\displaystyle x}$

${\displaystyle (k-1)mgx=(l/2-x)mg\подразумевает x=l/2k,}$

где обозначает гравитационное поле . Если верхние блоки выступают за центр масс на , то, принимая индуктивную гипотезу, максимальный выступ над столом равен${\displaystyle г}$${\displaystyle к-1}$${\displaystyle у}$

${\displaystyle y+{\frac {l}{2k}}=\sum _{i=1}^{k}{l/2i}\подразумевает y=\sum _{i=1}^{k-1}{l/2i}.}$

Для блоков обозначает, насколько верхние блоки выступают за центр масс , и . Тогда максимальный выступ будет равен:${\displaystyle к+1}$${\displaystyle у}$${\displaystyle к+1-1}$${\displaystyle (y=\sum _{i=1}^{k}l/2i)}$${\displaystyle x={\frac {l}{2(k+1)}}}$

${\displaystyle {\frac {l}{2(k+1)}}+\sum _{i=1}^{k}l/2i =\sum _{i=1}^{k+1}l /2i.}$

Холл (2005) обсуждает эту проблему, показывает, что она устойчива к неидеализациям, таким как скругленные углы блоков и конечная точность размещения блоков, и вводит несколько вариантов, включая ненулевые силы трения между соседними блоками.

• Холл, Дж. Ф. (2005). «Забава с укладкой блоков». Американский журнал физики . 73 (12): 1107–1116. Bibcode : 2005AmJPh..73.1107H. doi : 10.1119/1.2074007..
• Джонсон, Пол Б. (апрель 1955 г.). «Падающая башня Лира». Американский журнал физики . 23 (4): 240. Bibcode : 1955AmJPh..23..240J. doi : 10.1119/1.1933957.
• Патерсон, Майк ; Перес, Юваль ; Торуп, Миккель ; Винклер, Питер ; Цвик, Ури (2007). «Максимальный вылет». arXiv : 0707.0093 [math.HO].

• Вайсштейн, Эрик В. «Проблема укладки книг». MathWorld .
• «Строительство бесконечного моста». PBS Infinite Series . 2017-05-04 . Получено 2018-09-03 .