Критерий текучести Бигони–Пикколроаза
Критерий урожайности

Критерий текучести Бигони –Пикколроаза представляет собой модель текучести , основанную на феноменологическом подходе, способную описывать механическое поведение широкого класса чувствительных к давлению гранулированных материалов, таких как почва, бетон, пористые металлы и керамика.

Общие понятия

Процесс упрочнения при гидростатическом прессовании порошков описан с помощью поверхности текучести Бигони и Пикколроаза.

Идея критерия Бигони-Пикколроаза заключается в выводе функции, способной переходить между поверхностями текучести, типичными для различных классов материалов, только путем изменения параметров функции. [1] Причина такого рода реализации заключается в том, что материалы, на которые нацелена модель, претерпевают последовательные изменения в процессе производства и условий работы. Типичным примером является упрочнение образца энергетического назначения путем уплотнения и спекания, в ходе которого материал изменяется от зернистого до плотного.

Критерий текучести Бигони-Пикколроаза может быть представлен в пространстве напряжений Хейга-Вестергарда как выпуклая гладкая поверхность, и фактически сам критерий основан на математическом определении поверхности в вышеупомянутом пространстве как правильной интерполяции экспериментальных точек.

Математическая формулировка

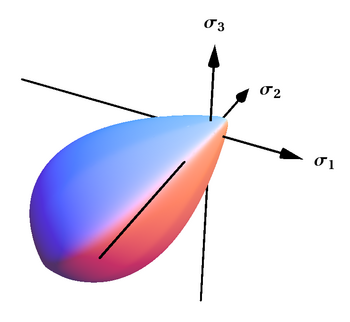
Поверхность текучести Бигони-Пикколроаза в трехмерном пространстве главных напряжений

Поверхность текучести Бигони-Пикколроаза рассматривается как прямая интерполяция экспериментальных данных. Этот критерий представляет собой гладкую и выпуклую поверхность, которая замкнута как при гидростатическом растяжении, так и при сжатии и имеет каплевидную форму, особенно подходящую для описания фрикционных и зернистых материалов. Этот критерий также был обобщен на случай поверхностей с углами. [2]

Принципы проектирования

Поскольку вся идея модели заключается в адаптации функции к экспериментальным данным , авторы выделили определенную группу признаков как желательные, даже если не обязательные, среди них:

  • гладкость поверхности;
  • возможность изменения формы и, следовательно, интерполяции на широкий класс экспериментальных данных для различных материалов;
  • возможность представления известных критериев с предельным набором параметров;
  • выпуклость поверхности.

Параметрическая функция

Представление координат и поверхности текучести BP в пространстве напряжений Хейга-Вестергаарда. п , д {\displaystyle p,q} θ {\displaystyle \тета}
Девиаторные сечения поверхности текучести БП.
Меридианные сечения поверхности текучести БП.

Критерий текучести Бигони–Пикколроаза представляет собой семипараметрическую поверхность, определяемую как:

ф ( п , д , θ ) = Ф ( п ) + д г ( θ ) = 0 , {\displaystyle f(p,q,\theta )=F(p)+{\frac {q}{g(\theta )}}=0,}

где p, q и — инварианты, зависящие от тензора напряжений , а — «меридиональная» функция: θ {\displaystyle \тета} Ф ( п ) {\displaystyle F(п)}

Ф ( п ) = { − М п с ( ϕ − ϕ м ) [ 2 ( 1 − α ) ϕ + α ] , ϕ ∈ [ 0 , 1 ] , + ∞ , ϕ ∉ [ 0 , 1 ] , {\displaystyle F(p)=\left\{{\begin{array}{ll}-Mp_{c}{\sqrt {(\phi -\phi ^{m})[2(1-\alpha )\phi +\alpha ]}},&\phi \in [0,1],\\+\infty ,&\phi \notin [0,1],\end{array}}\right.}
ϕ = п + с п с + с , {\displaystyle \phi = {\frac {p+c}{p_{c}+c}},}

описывающая чувствительность к давлению и являющаяся «девиаторной» функцией: [3] г ( θ ) {\displaystyle g(\theta)}

г ( θ ) = 1 потому что ⁡ [ β π 6 − 1 3 потому что − 1 ⁡ ( γ потому что ⁡ 3 θ ) ] , {\displaystyle g(\theta )={\frac {1}{\cos[\beta {\frac {\pi }{6}}-{\frac {1}{3}}\cos ^{-1}(\gamma \cos 3\theta )]}},}

описывающий зависимость текучести от Лоде.

Математические определения параметров и следующие: п , д {\displaystyle p,q} θ {\displaystyle \тета}

п = − т г   σ 3 , д = 3 Дж. 2 , θ = 1 3 с о с − 1 ( 3 3 2 Дж. 3 Дж. 2 3 / 2 ) {\displaystyle p=-{\frac {tr~\sigma}{3}},\quad q={\sqrt {3{\textit {J}}_{2}}},\quad \theta ={\frac {1}{3}}cos^{-1}\left({\frac {3{\sqrt {3}}}{2}}{\frac {J_{3}}{J_{2}^{3/2}}}\right)}

С:

Дж. 2 = 1 2 С ⋅ С , С = σ − т г   σ 3 я , Дж. 3 = 1 3 т г   С 3 {\displaystyle J_{2}={\frac {1}{2}}{\textbf {S}}\cdot {\textbf {S}},\quad {\textbf {S}}=\sigma -{\ frac {tr\ \sigma }{3}}{\textbf {I}},\quad J_{3}={\frac {1}{3}}tr\ {\textbf {S}}^{3}}

Где — девиаторное напряжение, — тензор тождественности, — тензор напряжений, а точка обозначает скалярное произведение. С {\displaystyle {\textbf {S}}} я {\displaystyle {\textbf {Я}}} σ {\displaystyle \сигма}

Лучшего понимания этих важных параметров можно достичь, используя их геометрическое представление в пространстве напряжений Хейга-Вестергаарда . [4] Рассматривая терм главных напряжений и девиаторную плоскость , ортогональную трисектору первого квадранта и проходящую через начало системы координат, терм и однозначно представляет точку в пространстве, действующую как цилиндрическая система координат с трисектором в качестве оси: π {\displaystyle \пи} п , д {\displaystyle p,q} θ {\displaystyle \тета}

  • − 3   п {\displaystyle -{\sqrt {3}}~p} - расстояние точки от девиаторной плоскости ; π {\displaystyle \пи}
  • 2 / 3   д {\displaystyle {\sqrt {2/3}}~q} — расстояние от трисектора;
  • θ {\displaystyle \тета} представляет собой угол между проекциями и осью на девиаторную плоскость . д {\displaystyle д} σ 1 {\displaystyle \сигма _{1}} π {\displaystyle \пи}

Использование p и q вместо правильных цилиндрических координат и : ξ {\displaystyle \xi} ρ {\displaystyle \ро}

ξ = 1 3 т г ( σ ) = − 3   п , ρ = 2   Дж. 2 = 2 3 д {\displaystyle \xi ={\frac {1}{\sqrt {3}}}tr(\sigma )=-{\sqrt {3}}~p,\quad \rho ={\sqrt {2~J_{2}}}={\sqrt {\frac {2}{3}}}q}

оправдывается более простой физической интерпретацией: [5] p — гидростатическое давление на материальную точку, q — эквивалентное напряжение по Мизесу.

Описанная функция текучести соответствует поверхности текучести:

д = − ф ( п ) г ( θ ) , п ∈ [ − с , п с ] , θ ∈ [ 0 , π / 3 ] {\displaystyle q=-f(p)g(\theta ),\quad p\in [-c,p_{c}],\quad \theta \in [0,\pi /3]}

что делает явной связь между двумя функциями и формой меридионального и девиаторного сечений соответственно. f ( p ) {\displaystyle f(p)} g ( θ ) {\displaystyle g(\theta )}

Семь неотрицательных материальных параметров:

M > 0 ,   p c > 0 ,   c ≥ 0 ,   0 < α < 2 ,   m > 1 ⏟ defining   F ( p ) ,       0 ≤ β ≤ 2 ,   0 ≤ γ < 1 ⏟ defining   g ( θ ) , {\displaystyle \underbrace {M>0,~p_{c}>0,~c\geq 0,~0<\alpha <2,~m>1} _{{\mbox{defining}}~\displaystyle {F(p)}},~~~\underbrace {0\leq \beta \leq 2,~0\leq \gamma <1} _{{\mbox{defining}}~\displaystyle {g(\theta )}},}

определяют форму меридиональных и девиаторных сечений. В частности, некоторые параметры легко соотносятся с механическими свойствами: контролирует чувствительность к давлению, и являются пределом текучести в изотропных условиях растяжения и сжатия. Другие параметры определяют форму поверхности при пересечении меридиональными и девиаторными плоскостями: и определяют меридиональное сечение, и определяют девиаторное сечение. M {\displaystyle M} c {\displaystyle c} p c {\displaystyle p_{c}} α {\displaystyle \alpha } m {\displaystyle m} β {\displaystyle \beta } γ {\displaystyle \gamma }

Поверхность текучести Бигони-Пикколроаза, разработанная для обеспечения согласованных изменений формы поверхности в пространстве напряжений Хейга-Вестергаарда , может использоваться в качестве обобщенной формулировки для нескольких критериев [6] , таких как хорошо известные критерии фон Мизеса , Трески , Мора-Кулона .

Смотрите также

Поверхность текучести Бигони-Пикколроаза является мощным инструментом для характеристики гранулированных материалов и вызывает большой интерес в области определения конститутивных моделей для керамики, горных пород и грунтов, что является задачей фундаментальной важности для лучшего проектирования изделий с использованием этих материалов.

  • https://bigoni.dicam.unitn.it/
  • https://apiccolroaz.dicam.unitn.it/
  • https://www.refracture2-h2020.eu/

Ссылки

  1. ^ Бигони, Д. и Пикколроаз, А., (2004), Критерии текучести для квазихрупких и фрикционных материалов, Международный журнал твердых тел и структур 41 , 2855–2878.
  2. ^ Пикколроаз, А. и Бигони, Д. (2009), Критерии текучести для квазихрупких и фрикционных материалов: обобщение для поверхностей с углами, Международный журнал твердых тел и структур 46 , 3587–3596.
  3. ^ Подгурский, Дж. (1984). Условие предельного состояния и функция диссипации для изотропных материалов. Архивы механики , 36 (3), стр. 323–342.
  4. ^ Нильс Саабье Оттосен, Матти Ристинмаа, 2005. Механика конститутивного моделирования, Elsevier, стр. 150-153.
  5. ^ Нето Перик Оуэн 2008 Вычислительные методы пластичности, Wiley стр. 157-165
  6. ^ Бигони, Д. Нелинейная механика твердого тела: теория бифуркаций и неустойчивость материалов. Cambridge University Press, 2012. ISBN  9781107025417 .
Retrieved from "https://en.wikipedia.org/w/index.php?title=Bigoni–Piccolroaz_yield_criterion&oldid=1248035214"