Дерево поведения (искусственный интеллект, робототехника и управление)
Математическая модель выполнения плана

Дерево поведения — это математическая модель выполнения плана , используемая в информатике , робототехнике , системах управления и видеоиграх . Они описывают переключения между конечным набором задач в модульной форме. Их сила заключается в их способности создавать очень сложные задачи, состоящие из простых задач, не беспокоясь о том, как простые задачи реализуются. Деревья поведения имеют некоторое сходство с иерархическими конечными автоматами с ключевым отличием, что основным строительным блоком поведения является задача, а не состояние. Его простота для человеческого понимания делает деревья поведения менее подверженными ошибкам и очень популярными в сообществе разработчиков игр. Было показано, что деревья поведения обобщают несколько других архитектур управления. [1] [2]

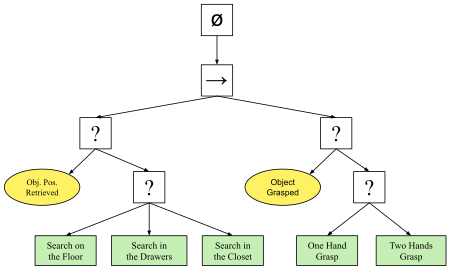
Дерево поведения, моделирующее план поиска и захвата двурукого робота

Фон

Первоначально структура управления на основе поведения была предложена Родни Бруксом в его статье под названием «Надежная многоуровневая система управления для мобильного робота». В первоначальном предложении список поведений мог работать как альтернатива друг другу, позже подход был расширен и обобщен в древовидной организации поведений с широким применением в игровой индустрии [ требуется ссылка ] в качестве мощного инструмента для моделирования поведения неигровых персонажей (NPC). [3] [4] [5] [6] Они широко использовались в известных видеоиграх, таких как Halo , Bioshock и Spore . В недавних работах деревья поведения предлагаются в качестве многоцелевой структуры управления для БПЛА , сложных роботов, роботизированной манипуляции и многороботных систем. [7] [8] [9] [10] [11] [12] Деревья поведения теперь достигли той зрелости, что их можно рассматривать в учебниках по игровому ИИ, [13] [14], а также в общих игровых средах, таких как Unity (игровой движок) и Unreal Engine (см. ссылки ниже).

Деревья поведения стали популярными благодаря своей парадигме разработки: возможность создания сложного поведения путем программирования только действий NPC, а затем проектирования древовидной структуры (обычно с помощью перетаскивания ), конечные узлы которой являются действиями, а внутренние узлы определяют принятие решений NPC. Деревья поведения визуально интуитивно понятны и просты в проектировании, тестировании и отладке, а также обеспечивают большую модульность, масштабируемость и возможность повторного использования, чем другие методы создания поведения.

На протяжении многих лет различные реализации деревьев поведения продолжали совершенствоваться как по эффективности, так и по возможностям для удовлетворения потребностей отрасли, пока они не превратились в деревья поведения, управляемые событиями . [15] [5] Деревья поведения, управляемые событиями, решили некоторые проблемы масштабируемости классических деревьев поведения, изменив то, как дерево внутренне обрабатывает свое выполнение, и введя новый тип узла, который может реагировать на события и прерывать выполнение узлов. В настоящее время концепция дерева поведения, управляемого событиями, является стандартом и используется в большинстве реализаций, хотя для простоты их по-прежнему называют «деревьями поведения».

Ключевые понятия

Дерево поведения графически представлено как направленное дерево , в котором узлы классифицируются как корневые, узлы потока управления или узлы выполнения (задачи). Для каждой пары связанных узлов исходящий узел называется родительским, а входящий узел называется дочерним. Корень не имеет родителей и ровно одного дочернего узла, узлы потока управления имеют одного родителя и по крайней мере одного дочернего узла, а узлы выполнения имеют одного родителя и ни одного дочернего узла. Графически дочерние узлы узла потока управления располагаются под ним, упорядоченные слева направо. [16]

Выполнение дерева поведения начинается с корня, который с определенной частотой посылает такты своему потомку. Такт — это разрешающий сигнал, который разрешает выполнение потомка. Когда выполнение узла в дереве поведения разрешено, он возвращает родителю статус running , если его выполнение еще не завершено, success , если он достиг своей цели, или failure в противном случае.

Узел потока управления

Узел потока управления используется для управления подзадачами, из которых он состоит. Узел потока управления может быть либо узлом выбора (резервным), либо узлом последовательности. Они запускают каждую из своих подзадач по очереди. Когда подзадача завершена и возвращает свой статус (успех или неудача), узел потока управления решает, выполнять ли следующую подзадачу или нет.

Узел выбора (резервный)

Рисунок I. Графическое представление резервной композиции из N задач.

Узлы отката используются для поиска и выполнения первого дочернего узла, который не дает сбой. Узел отката немедленно вернется с кодом статуса успеха или выполнения, когда один из его дочерних узлов вернет успех или выполнение (см. рисунок I и псевдокод ниже). Дочерние узлы отмечены в порядке важности слева направо.

В псевдокоде алгоритм резервной композиции выглядит следующим образом:

1 для i от 1 до n сделать2 childstatus ← Отметить(ребенок(i))3 если childstatus = работает4 обратный ход5 иначе, если childstatus = успех6 возвращение успеха7 конец
8 возврат неудача

Узел последовательности

Рисунок II. Графическое представление последовательности из N задач.

Узлы последовательности используются для поиска и выполнения первого дочернего элемента, который еще не был успешно выполнен. Узел последовательности немедленно вернется с кодом состояния «неудача» или «выполнение», когда один из его дочерних элементов вернет «неудача» или «выполнение» (см. рисунок II и псевдокод ниже). Дочерние элементы отмечены по порядку слева направо.

В псевдокоде алгоритм построения последовательности выглядит следующим образом:

1 для i от 1 до n сделать2 childstatus ← Отметить(ребенок(i))3 если childstatus = работает4 обратный ход5 иначе, если childstatus = неудача6 отказ возврата7 конец
8 возвращение успеха

Определение математического пространства состояний

Чтобы применить инструменты теории управления к анализу деревьев поведения, их можно определить как трехкортежные. [17]

Т я = { ф я , г я , Δ т } , {\displaystyle T_{i}=\{f_{i},r_{i},\Delta t\},}

где — индекс дерева, — векторное поле, представляющее правую часть обыкновенного разностного уравнения, — временной шаг, а — статус возврата, который может быть равен Running , Success или Failure . я ∈ Н {\displaystyle i\in \mathbb {N} } ф я : Р н → Р н {\displaystyle f_{i}:\mathbb {R} ^{n}\rightarrow \mathbb {R} ^{n}} Δ т {\displaystyle \Дельта t} г я : Р н → { Р я , С я , Ф я } {\displaystyle r_{i}:\mathbb {R} ^{n}\rightarrow \{R_{i},S_{i},F_{i}\}} Р я {\displaystyle R_{i}} С я {\displaystyle S_{i}} Ф я {\displaystyle F_{i}}

Примечание : Задача представляет собой вырожденное дерево поведения, не имеющее родителя и потомка.

Выполнение дерева поведения

Выполнение дерева поведения описывается следующими стандартными обыкновенными разностными уравнениями:

х к + 1 ( т к + 1 ) = ф я ( х к ( т к ) ) {\displaystyle x_{k+1}(t_{k+1})=f_{i}(x_{k}(t_{k}))}

т к + 1 = т к + Δ т {\displaystyle t_{k+1}=t_{k}+\Дельта t}

где представляют собой дискретное время, а — пространство состояний системы, моделируемое деревом поведения. к ∈ Н {\displaystyle k\in \mathbb {N} } х ∈ Р н {\displaystyle x\in \mathbb {R} ^{n}}

Последовательность композиции

Два дерева поведения можно объединить в более сложное дерево поведения с помощью оператора последовательности. Т я {\displaystyle T_{i}} Т дж {\displaystyle T_{j}} Т 0 {\displaystyle T_{0}}

Т 0 = последовательность ( Т я , Т дж ) . {\displaystyle T_{0}={\mbox{последовательность}}(T_{i},T_{j}).}

Затем возвращаемый статус и связанное с ним векторное поле определяются (для [ необходимо определение ] ) следующим образом: г 0 {\displaystyle r_{0}} ф 0 {\displaystyle f_{0}} Т 0 {\displaystyle T_{0}} С 1 {\displaystyle {\mathcal {S}}_{1}}

г 0 ( х к ) = { г дж ( х к )  если  х к ∈ С 1 г я ( х к )  в противном случае  . {\displaystyle r_{0}(x_{k})={\begin{cases}r_{j}(x_{k})&{\text{ если }}x_{k}\in {\mathcal {S}}_{1}\\r_{i}(x_{k})&{\text{ в противном случае }}.\end{cases}}}

ф 0 ( х к ) = { ф дж ( х к )  если  х к ∈ С 1 ф я ( х к )  в противном случае  . {\displaystyle f_{0}(x_{k})={\begin{cases}f_{j}(x_{k})&{\text{ если }}x_{k}\in {\mathcal {S}}_{1}\\f_{i}(x_{k})&{\text{ в противном случае }}.\end{cases}}}

Смотрите также

Ссылки

  1. ^ Колледанчайз, Мишель; Огрен, Петтер (2017). «Как деревья поведения модуляризируют гибридные системы управления и обобщают последовательные композиции поведения, архитектуру подчинения и деревья решений». Труды IEEE по робототехнике . 33 (2): 372– 389. doi :10.1109/TRO.2016.2633567. S2CID  9518238.
  2. ^ Колледанчиз, Мишель; Огрен, Петтер (2018). Деревья поведения в робототехнике и искусственном интеллекте: введение . ЦРК Пресс. arXiv : 1709.00084 . дои : 10.1201/9780429489105. ISBN 978-1-138-59373-2. S2CID  27470659.
  3. ^ Айла, Д. (2005). «Управление сложностью в ИИ Halo 2». Game Developers Conference (т. 12) .
  4. ^ Айла, Д. (2008). Halo 3 — создание лучшего боя . {{cite book}}: |work=проигнорировано ( помощь )
  5. ^ ab Agis, Ramiro A.; Gottifredi, Sebastian; García, Alejandro J. (2020). «Расширение деревьев поведения, управляемое событиями, для облегчения многоагентной координации без участия игрока в видеоиграх» (PDF) . Expert Systems with Applications . 155 (1): 113457. doi :10.1016/j.eswa.2020.113457. S2CID  218995637.
  6. ^ Lim, CU; Baumgarten, R.; Colton, S. (2010). "Evolving Behaviour Trees for the Commercial Game DEFCON" (PDF) . Applications of Evolutionary Computing . Lecture Notes in Computer Science. Vol. 6024. Berlin: Springer. pp.  100– 110. doi :10.1007/978-3-642-12239-2_11. ISBN 978-3-642-12238-5.
  7. ^ Огрен, Петтер (2012). «Повышение модульности систем управления БПЛА с использованием деревьев поведения компьютерной игры» (PDF) . Конференция AIAA по наведению, навигации и управлению, Миннеаполис, Миннесота . С.  13–16 .
  8. ^ Колледанчизе, Микеле; Марзинотто, Алехандро; Огрен, Петтер (2014). «Анализ производительности деревьев стохастического поведения» (PDF) . Международная конференция IEEE по робототехнике и автоматизации (ICRA) 2014 г. стр.  3265–3272 . doi :10.1109/ICRA.2014.6907328. ISBN 978-1-4799-3685-4. S2CID  14719083.
  9. ^ Марзинотто, Алехандро; Колледанчизе, Мишель; Смит, Кристиан; Огрен, Петтер (2014). «На пути к унифицированной структуре BT для управления роботом» (PDF) . Робототехника и автоматизация (ICRA), Международная конференция IEEE 2014 г.
  10. ^ Клёкнер, Андреас. «Взаимодействие БТ с миром с использованием логики описания». На конференции AIAA по руководству, навигации и управлению, Бостон, Массачусетс. 2013.
  11. ^ Клёкнер, Андреас (2013). «Деревья поведения для управления миссиями БПЛА». GI-Jahretagung . стр.  57–68 .
  12. ^ Багнелл, Дж. Эндрю; Кавальканти, Фелипе; Куи, Лей; и др. (2012). «Интегрированная система для автономной робототехнической манипуляции» (PDF) . Интеллектуальные роботы и системы (IROS), 2012 IEEE/RSJ Международная конференция по . IEEE. стр.  2955– 2962. doi :10.1109/IROS.2012.6385888. hdl :20.500.11937/14608. ISBN 978-1-4673-1736-8. S2CID  419179.
  13. ^ Миллингтон; Funge (2009). Искусственный интеллект для игр . CRC Press. ISBN 978-0-12-374731-0.
  14. ^ Рабин, С. (2014). Game AI Pro . CRC Press. ISBN 978-1-4665-6596-8.
  15. ^ Шампандар, Алекс Дж.; Данстан, Филип (2012). «Начальный комплект Behavior Tree» (PDF) . Game AI Pro: Собрание мудрости профессионалов в области игрового ИИ . С.  72–92 .
  16. ^ craft ai (2015). «BT 101 – Основы грамматики деревьев поведения».
  17. ^ Колледанчайз, Мишель; Огрен, Петтер (2014). «Как деревья поведения модулируют надежность и безопасность в гибридных системах» (PDF) . В «Интеллектуальных роботах и ​​системах» (IROS), Международная конференция IEEE/RSJ 2014 г. по . IEEE.
  • Библиотека дерева поведения ROS
  • Документация по поведению дерева Unreal Engine 4
  • Деревья поведения для ИИ: как они работают
  • Деревья поведения: простой, но мощный ИИ для вашего робота Архивировано 25.02.2020 на Wayback Machine
  • Видеолекции по деревьям поведения
Взято с "https://en.wikipedia.org/w/index.php?title=Дерево_поведения_(искусственный_интеллект,_робототехника_и_управление)&oldid=1214363898"