Альтернативное дерево решений

Альтернативное дерево решений (ADTree) — это метод машинного обучения для классификации. Он обобщает деревья решений и имеет связи с бустингом .

ADTree состоит из чередования узлов решений, которые определяют условие предиката, и узлов прогнозирования, которые содержат одно число. Экземпляр классифицируется ADTree путем следования всем путям, для которых все узлы решений являются истинными, и суммирования любых пройденных узлов прогнозирования.

История

ADTrees были введены Йоавом Фройндом и Лью Мейсоном. [1] Однако представленный алгоритм имел несколько типографских ошибок. Разъяснения и оптимизации были позже представлены Бернхардом Пфарингером, Джеффри Холмсом и Ричардом Киркби. [2] Реализации доступны в Weka и JBoost.

Мотивация

Первоначальные алгоритмы повышения обычно использовали либо пни решений , либо деревья решений в качестве слабых гипотез. Например, пни решений повышения создают набор взвешенных пней решений (где — число итераций повышения), которые затем голосуют за окончательную классификацию в соответствии со своими весами. Отдельные пни решений взвешиваются в соответствии с их способностью классифицировать данные. Т {\displaystyle Т} Т {\displaystyle Т}

Усиление простого обучающегося приводит к неструктурированному набору гипотез, что затрудняет вывод корреляций между атрибутами. Чередующиеся деревья решений вводят структуру в набор гипотез, требуя, чтобы они строились на гипотезе, которая была создана в более ранней итерации. Результирующий набор гипотез можно визуализировать в дереве, основанном на связи между гипотезой и ее «родителем». Т {\displaystyle Т}

Еще одной важной особенностью усиленных алгоритмов является то, что данные получают разное распределение на каждой итерации. Экземпляры, которые классифицированы неправильно, получают больший вес, в то время как точно классифицированные экземпляры получают меньший вес.

Альтернативная структура дерева решений

Переменное дерево решений состоит из узлов решений и узлов прогнозирования. Узлы решений определяют предикатное условие. Узлы прогнозирования содержат одно число. ADTrees всегда имеют узлы прогнозирования как в качестве корня, так и листьев. Экземпляр классифицируется ADTree путем следования всем путям, для которых все узлы решений являются истинными, и суммирования всех пройденных узлов прогнозирования. Это отличается от бинарных деревьев классификации, таких как CART ( дерево классификации и регрессии ) или C4.5 , в которых экземпляр следует только одному пути по дереву.

Пример

Следующее дерево было построено с использованием JBoost на основе набора данных spambase [3] (доступного в репозитории машинного обучения UCI). [4] В этом примере спам кодируется как1 и обычная электронная почта кодируется как−1 .

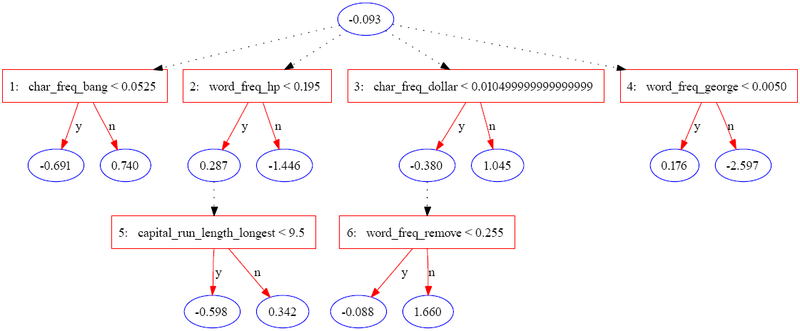
ADTree для 6 итераций на наборе данных Spambase.
ADTree для 6 итераций на наборе данных Spambase.

В следующей таблице содержится часть информации для одного экземпляра.

Экземпляр, подлежащий классификации
ОсобенностьЦенить
char_freq_bang0,08
word_freq_hp0.4
capital_run_length_longest4
char_freq_dollar0
word_freq_remove0.9
word_freq_george0
Другие особенности...

Экземпляр оценивается путем суммирования всех узлов прогнозирования, через которые он проходит. В случае экземпляра выше оценка вычисляется как

Оценка для приведенного выше примера
Итерация0123456
Значения экземпляра—.08 < .052 = ф.4 < .195 = ф0 < .01 = т0 < 0,005 = т—.9 < .225 = ф
Прогноз-0,0930,74-1.446-0,380,17601.66

Окончательный счет0,657 положительно, поэтому экземпляр классифицируется как спам. Величина значения является мерой уверенности в прогнозе. Первоначальные авторы перечисляют три потенциальных уровня интерпретации для набора атрибутов, идентифицированных ADTree:

  • Отдельные узлы можно оценить по их собственной прогностической способности.
  • Наборы узлов на одном и том же пути можно интерпретировать как имеющие совместный эффект.
  • Дерево можно интерпретировать как единое целое.

При интерпретации отдельных узлов следует соблюдать осторожность, поскольку оценки отражают переоценку данных в каждой итерации.

Описание алгоритма

Входные данные для алгоритма переменного дерева решений:

  • Набор входных данных , где — вектор атрибутов, равный либо -1, либо 1. Входные данные также называются экземплярами. ( х 1 , у 1 ) , … , ( х м , у м ) {\displaystyle (x_{1},y_{1}),\ldots ,(x_{m},y_{m})} х я {\displaystyle x_{i}} у я {\displaystyle y_{i}}
  • Набор весов, соответствующих каждому экземпляру. ж я {\displaystyle w_{i}}

Основным элементом алгоритма ADTree является правило. Одно правило состоит из предусловия, условия и двух оценок. Условие — это предикат формы «атрибут <сравнение> значение». Предусловие — это просто логическое соединение условий. Оценка правила включает пару вложенных операторов if:

1 если (предварительное условие)2 если (условие)3 вернуть счет_один4 еще
5 вернуть счет_два6 конец, если
7 иначе
8 вернуть 09 конец если

Алгоритму также требуются несколько вспомогательных функций:

  • Вт + ( с ) {\displaystyle W_{+}(с)} возвращает сумму весов всех положительно помеченных примеров, которые удовлетворяют предикату с {\displaystyle с}
  • Вт − ( с ) {\displaystyle W_{-}(c)} возвращает сумму весов всех отрицательно помеченных примеров, которые удовлетворяют предикату с {\displaystyle с}
  • Вт ( с ) = Вт + ( с ) + Вт − ( с ) {\displaystyle W(c)=W_{+}(c)+W_{-}(c)} возвращает сумму весов всех примеров, удовлетворяющих предикату с {\displaystyle с}

Алгоритм следующий:

1 функция ad_tree2 входных набора из m обучающих примеров34 w i = 1/ m для всех i
5
6 R 0 = правило с оценками a и 0 , предусловием «истина» и условием «истина».    а =   1 2     вн       Вт  +   ( т г ты е )    Вт  −   ( т г ты е )      {\displaystyle a={\frac {1}{2}}{\textrm {ln}}{\frac {W_{+}(true)}{W_{-}(true)}}} 7
8 набор всех возможных условий
9 для
10 получить значения , которые минимизируют
11
12
13
14 R j = новое правило с предусловием p , условием c и весами a 1 и a 2
15
16 конец для
17 вернуть набор R j      П   = { т г ты е }   {\displaystyle {\mathcal {P}}=\{true\}}       С   =   {\displaystyle {\mathcal {C}}=}      дж = 1 … Т   {\displaystyle j=1\точки T}     п ∈   П   , с ∈   С     {\displaystyle p\in {\mathcal {P}},c\in {\mathcal {C}}}      з = 2  (     Вт  +   ( п ∧ с )  Вт  −   ( п ∧ с )   +    Вт  +   ( п ∧ ¬ с )  Вт  −   ( п ∧ ¬ с )    )  + Вт ( ¬ п )   {\displaystyle z=2\left({\sqrt {W_{+}(p\клин c)W_{-}(p\клин c)}}+{\sqrt {W_{+}(p\клин \отрицательный c)W_{-}(p\клин \отрицательный c)}}\right)+W(\отрицательный p)}       П   + = п ∧ с + п ∧ ¬ с   {\displaystyle {\mathcal {P}}+=p\клин с+p\клин \отрицательный с}      а  1   =   1 2     вн       Вт  +   ( п ∧ с ) + 1    Вт  −   ( п ∧ с ) + 1      {\displaystyle a_{1}={\frac {1}{2}}{\textrm {ln}}{\frac {W_{+}(p\клин c)+1}{W_{-}(p\клин c)+1}}}      а  2   =   1 2     вн       Вт  +   ( п ∧ ¬ с ) + 1    Вт  −   ( п ∧ ¬ с ) + 1      {\displaystyle a_{2}={\frac {1}{2}}{\textrm {ln}}{\frac {W_{+}(p\клин \отрицательный c)+1}{W_{-}(p\клин \отрицательный c)+1}}}      ж  я   =  ж  я    е  −  у  я    Р  дж   (  х  я   )     {\displaystyle w_{i}=w_{i}e^{-y_{i}R_{j}(x_{i})}}

Набор увеличивается на два предварительных условия в каждой итерации, и можно вывести древовидную структуру набора правил, отметив предварительные условия, которые используются в каждом последующем правиле. П {\displaystyle {\mathcal {P}}}

Эмпирические результаты

Рисунок 6 в оригинальной статье [1] демонстрирует, что ADTrees обычно так же надежны, как усиленные деревья решений и усиленные пни решений . Обычно эквивалентная точность может быть достигнута с гораздо более простой структурой дерева, чем рекурсивные алгоритмы разбиения.

Ссылки

  1. ^ ab Freund, Y.; Mason, L. (1999). "Алгоритм обучения на основе чередующегося дерева решений" (PDF) . Труды Шестнадцатой международной конференции по машинному обучению (ICML '99). Morgan Kaufmann. стр.  124–133 . ISBN 978-1-55860-612-8.
  2. ^ Пфарингер, Бернхард; Холмс, Джеффри; Киркби, Ричард (2001). «Оптимизация индукции чередующихся деревьев решений» (PDF) . Достижения в области обнаружения знаний и добычи данных. PAKDD 2001. Конспект лекций по информатике. Том 2035. Springer. С.  477– 487. doi :10.1007/3-540-45357-1_50. ISBN 978-3-540-45357-4.
  3. ^ "Набор данных Spambase". Репозиторий машинного обучения UCI . 1999.
  4. ^ Дуа, Д.; Графф, К. (2019). «Репозиторий машинного обучения UCI». Калифорнийский университет в Ирвайне, Школа информации и компьютерных наук.
  • Введение в Boosting и ADTrees (содержит множество графических примеров альтернативных деревьев решений на практике).
  • Программное обеспечение JBoost, реализующее ADTrees.
Взято с "https://en.wikipedia.org/w/index.php?title=Чередованное_дерево_решений&oldid=1131331915"