Расширенный стандарт шифрования
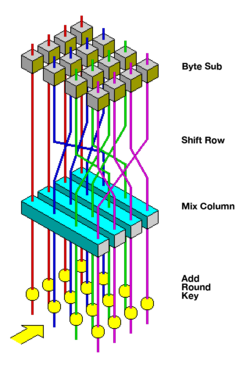 Визуализация функции раунда AES | |
| Общий | |
|---|---|
| Дизайнеры | Джоан Дэймен , Винсент Реймен |
| Впервые опубликовано | 1998 |
| Получено из | Квадрат |
| Преемники | Анубис , Гран Крю , Калина |
| Сертификация | Победитель AES , CRYPTREC , NESSIE , АНБ |
| Детали шифра | |
| Размеры клавиш | 128, 192 или 256 бит [примечание 1] |
| Размеры блоков | 128 бит [примечание 2] |
| Структура | Сеть подстановки-перестановки |
| Раунды | 10, 12 или 14 (в зависимости от размера ключа) |
| Лучший публичный криптоанализ | |
| Были опубликованы атаки, которые в вычислительном отношении быстрее, чем атака методом полного перебора , хотя по состоянию на 2023 год ни одна из них не является вычислительно осуществимой. [1] Для AES-128 ключ может быть восстановлен с вычислительной сложностью 2 126,1 с использованием атаки biclique . Для атак biclique на AES-192 и AES-256 применяются вычислительные сложности 2 189,7 и 2 254,4 соответственно. Атаки со связанными ключами могут взломать AES-256 и AES-192 со сложностью 2 99,5 и 2 176 как по времени, так и по данным соответственно. [2] Другая атака была описана в блоге [3] и выпущена в виде препринта [4] в 2009 году. Эта атака направлена против AES-256, который использует только два связанных ключа и 2,39 времени для восстановления полного 256-битного ключа 9-раундовой версии, или 2,45 времени для 10-раундовой версии с более сильным типом связанной атаки на подключ, или 2,70 времени для 11-раундовой версии. | |
Расширенный стандарт шифрования ( AES ), также известный под своим первоначальным названием Rijndael ( голландское произношение: [ˈrɛindaːl] ), [5] представляет собой спецификацию шифрования электронных данных, установленную Национальным институтом стандартов и технологий США (NIST) в 2001 году. [6]
AES — это вариант блочного шифра Rijndael [5], разработанный двумя бельгийскими криптографами, Джоаном Даеменом и Винсентом Рейменом , которые представили предложение [7] в NIST во время процесса отбора AES . [8] Rijndael — это семейство шифров с разными размерами ключей и блоков. Для AES NIST выбрал три члена семейства Rijndael, каждый с размером блока 128 бит, но тремя разными длинами ключей: 128, 192 и 256 бит.
AES был принят правительством США . Он заменяет стандарт шифрования данных (DES), [9] , опубликованный в 1977 году. Алгоритм, описанный AES, является алгоритмом с симметричным ключом , что означает, что один и тот же ключ используется как для шифрования, так и для дешифрования данных.
В Соединенных Штатах AES был объявлен NIST как US FIPS PUB 197 (FIPS 197) 26 ноября 2001 года. [6] Это объявление последовало за пятилетним процессом стандартизации, в ходе которого были представлены и оценены пятнадцать конкурирующих проектов, прежде чем шифр Rijndael был выбран как наиболее подходящий. [примечание 3]
AES включен в стандарт ISO / IEC 18033-3 . AES вступил в силу в качестве федерального правительственного стандарта США 26 мая 2002 года после одобрения министром торговли США Дональдом Эвансом . AES доступен во многих различных пакетах шифрования и является первым (и единственным) общедоступным шифром, одобренным Агентством национальной безопасности США (АНБ) для совершенно секретной информации при использовании в одобренном АНБ криптографическом модуле. [примечание 4]
Окончательные стандарты
Расширенный стандарт шифрования (AES) определен в каждом из следующих документов:
- FIPS PUB 197: Расширенный стандарт шифрования (AES) [6]
- ISO/IEC 18033-3: Блочные шифры [10]
Описание шифров
AES основан на принципе проектирования, известном как сеть подстановки-перестановки , и эффективен как в программном, так и в аппаратном обеспечении. [11] В отличие от своего предшественника DES, AES не использует сеть Фейстеля . AES является вариантом Rijndael с фиксированным размером блока 128 бит и размером ключа 128, 192 или 256 бит. Напротив, Rijndael как таковой указан с размерами блока и ключа, которые могут быть любыми кратными 32 битам, с минимальным значением 128 и максимальным значением 256 бит. Большинство вычислений AES выполняются в определенном конечном поле .
AES работает с массивом 4 × 4 столбцового порядка из 16 байт b 0 , b 1 , ..., b 15 , называемым состоянием : [примечание 5]
Размер ключа, используемый для шифра AES, определяет количество раундов преобразования, которые преобразуют входные данные, называемые открытым текстом , в конечные выходные данные, называемые зашифрованным текстом . Количество раундов следующее:
- 10 раундов для 128-битных ключей.
- 12 раундов для 192-битных ключей.
- 14 раундов для 256-битных ключей.
Каждый раунд состоит из нескольких этапов обработки, включая тот, который зависит от самого ключа шифрования. Набор обратных раундов применяется для преобразования зашифрованного текста обратно в исходный открытый текст с использованием того же ключа шифрования.
Высокоуровневое описание алгоритма
- KeyExpansion – ключи раунда выводятся из ключа шифрования с использованием расписания ключей AES . AES требует отдельный 128-битный блок ключа раунда для каждого раунда плюс еще один.
- Добавление ключа начального раунда:
- AddRoundKey – каждый байт состояния объединяется с байтом раундового ключа с помощью побитового xor .
- 9, 11 или 13 раундов:
- SubBytes – шаг нелинейной замены, при котором каждый байт заменяется другим в соответствии с таблицей поиска .
- ShiftRows – шаг транспонирования, при котором последние три строки состояния циклически сдвигаются на определенное количество шагов.
- MixColumns – линейная операция смешивания, которая работает со столбцами состояния, объединяя четыре байта в каждом столбце.
- AddRoundKey
- Финальный раунд (всего 10, 12 или 14 раундов):
- Суббайты
- ShiftRows
- AddRoundKey
TheСуббайтышаг
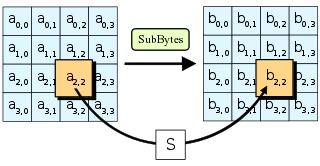
На шаге SubBytes каждый байт в массиве состояний заменяется на SubByte с использованием 8-битного блока подстановки . Перед раундом 0 массив состояний представляет собой просто открытый текст/вход. Эта операция обеспечивает нелинейность в шифре . Используемый S-box выводится из мультипликативной инверсии над GF (2 8 ) , которая, как известно, имеет хорошие свойства нелинейности. Чтобы избежать атак, основанных на простых алгебраических свойствах, S-box создается путем объединения обратной функции с обратимым аффинным преобразованием . S-box также выбирается так, чтобы избегать любых неподвижных точек (и, следовательно, расстройства ) , т. е. , а также любых противоположных неподвижных точек, т. е . . При выполнении расшифровки используется шаг InvSubBytes (обратный SubBytes ), который требует сначала взять инверсию аффинного преобразования, а затем найти мультипликативную инверсию.
TheShiftRowsшаг
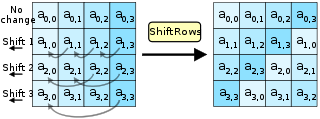
Шаг ShiftRows работает со строками состояния; он циклически сдвигает байты в каждой строке на определенное смещение . Для AES первая строка остается неизменной. Каждый байт второй строки сдвигается на один влево. Аналогично третья и четвертая строки сдвигаются на смещения два и три соответственно. [примечание 6] Таким образом, каждый столбец выходного состояния шага ShiftRows состоит из байтов из каждого столбца входного состояния. Важность этого шага заключается в том, чтобы избежать независимого шифрования столбцов, в этом случае AES выродится в четыре независимых блочных шифра.
TheMixColumnsшаг
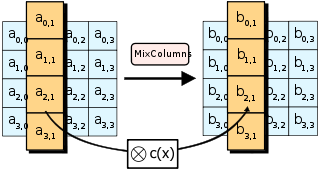
На этапе MixColumns четыре байта каждого столбца состояния объединяются с помощью обратимого линейного преобразования . Функция MixColumns принимает четыре байта в качестве входных данных и выводит четыре байта, где каждый входной байт влияет на все четыре выходных байта. Вместе с ShiftRows MixColumns обеспечивает диффузию в шифре.
Во время этой операции каждый столбец преобразуется с использованием фиксированной матрицы (матрица, умноженная слева на столбец, дает новое значение столбца в состоянии):
Умножение матриц состоит из умножения и сложения записей. Записи — это байты, рассматриваемые как коэффициенты полинома порядка . Сложение — это просто XOR. Умножение — это модуль неприводимого полинома . Если обрабатывать побитно, то после сдвига следует выполнить условный XOR с 1B 16 , если сдвинутое значение больше FF 16 (переполнение должно быть исправлено вычитанием порождающего полинома). Это особые случаи обычного умножения в .
В более общем смысле каждый столбец рассматривается как полином над и затем умножается по модулю на фиксированный полином . Коэффициенты отображаются в их шестнадцатеричном эквиваленте двоичного представления битовых полиномов из . Шаг MixColumns также можно рассматривать как умножение на показанную конкретную матрицу MDS в конечном поле . Этот процесс подробно описан в статье Rijndael MixColumns .
TheAddRoundKey
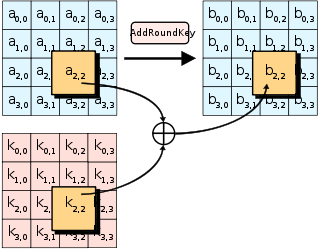
На шаге AddRoundKey подключаемый ключ объединяется с состоянием. Для каждого раунда подключаемый ключ выводится из основного ключа с использованием ключевого расписания Rijndael ; каждый подключаемый ключ имеет тот же размер, что и состояние. Подключ добавляется путем объединения состояния с соответствующим байтом подключаемого ключа с использованием побитового XOR .
Оптимизация шифра
В системах с 32-битными или более длинными словами можно ускорить выполнение этого шифра, объединив шаги SubBytes и ShiftRows с шагом MixColumns , преобразовав их в последовательность табличных поисков. Для этого требуются четыре 256-записных 32-битных таблицы (вместе занимающие 4096 байт). Затем раунд может быть выполнен с 16 операциями табличного поиска и 12 32-битными операциями исключающего ИЛИ, за которыми следуют четыре 32-битных операции исключающего ИЛИ на шаге AddRoundKey . [12] В качестве альтернативы, операция табличного поиска может быть выполнена с одной 256-записной 32-битной таблицей (занимающей 1024 байта), за которой следуют операции циклического вращения.
Используя байт-ориентированный подход, можно объединить шаги SubBytes , ShiftRows и MixColumns в одну раундовую операцию. [13]
Безопасность
Агентство национальной безопасности (АНБ) рассмотрело всех финалистов AES, включая Rijndael, и заявило, что все они достаточно безопасны для несекретных данных правительства США. В июне 2003 года правительство США объявило, что AES может использоваться для защиты секретной информации :
Конструкция и стойкость всех длин ключей алгоритма AES (т. е. 128, 192 и 256) достаточны для защиты секретной информации вплоть до уровня СЕКРЕТНО. Для совершенно СЕКРЕТНОЙ информации потребуется использовать ключи длиной 192 или 256. Внедрение AES в продукты, предназначенные для защиты систем национальной безопасности и/или информации, должно быть рассмотрено и сертифицировано АНБ до их приобретения и использования. [14]
AES имеет 10 раундов для 128-битных ключей, 12 раундов для 192-битных ключей и 14 раундов для 256-битных ключей.
К 2006 году наиболее известными атаками были 7 раундов для 128-битных ключей, 8 раундов для 192-битных ключей и 9 раундов для 256-битных ключей. [15]
Известные атаки
Для криптографов криптографический «взлом» — это все, что быстрее атаки методом перебора — т. е. выполнение одной пробной расшифровки для каждого возможного ключа в последовательности . Таким образом, взлом может включать результаты, которые невозможны с использованием современных технологий. Несмотря на свою непрактичность, теоретические взломы иногда могут дать представление о моделях уязвимостей. Самая крупная успешная публично известная атака методом перебора против широко распространенного алгоритма шифрования блочным шифром была проведена против 64-битного ключа RC5 компанией distributed.net в 2006 году. [16]
Пространство ключей увеличивается в 2 раза для каждого дополнительного бита длины ключа, и если каждое возможное значение ключа равновероятно; это означает удвоение среднего времени поиска ключа методом перебора с каждым дополнительным битом длины ключа. Это означает, что усилие поиска методом перебора экспоненциально увеличивается с длиной ключа. Длина ключа сама по себе не подразумевает защищенность от атак, поскольку существуют шифры с очень длинными ключами, которые оказались уязвимыми.
AES имеет довольно простую алгебраическую структуру. [17] В 2002 году Николя Куртуа и Йозеф Пиепшик объявили о теоретической атаке, названной « атакой XSL » , которая якобы показывала слабость алгоритма AES, частично из-за низкой сложности его нелинейных компонентов. [18] С тех пор другие статьи показали, что атака, как она была первоначально представлена, неработоспособна; см. Атака XSL на блочные шифры .
В процессе отбора AES разработчики конкурирующих алгоритмов писали об алгоритме Rijndael: «Мы обеспокоены [его] использованием... в приложениях, критически важных для безопасности». [19] Однако в октябре 2000 года в конце процесса отбора AES Брюс Шнайер , разработчик конкурирующего алгоритма Twofish , написал, что, хотя он и думал, что когда-нибудь будут разработаны успешные академические атаки на Rijndael, он «не верил, что кто-то когда-нибудь обнаружит атаку, которая позволит кому-то читать трафик Rijndael». [20]
До мая 2009 года единственными успешными опубликованными атаками против полного AES были атаки по сторонним каналам на некоторые конкретные реализации. В 2009 году была обнаружена новая атака со связанными ключами , которая использует простоту ключевого расписания AES и имеет сложность 2 119 . В декабре 2009 года она была улучшена до 2 99,5 . [2] Это продолжение атаки, обнаруженной ранее в 2009 году Алексом Бирюковым , Дмитрием Ховратовичем и Ивицей Николичем, со сложностью 2 96 для одного из каждых 2 35 ключей. [21] Однако атаки со связанными ключами не представляют интереса ни для одного правильно разработанного криптографического протокола, поскольку правильно разработанный протокол (т. е. имплементационное программное обеспечение) позаботится о том, чтобы не допустить связанных ключей, по сути, ограничивая средства злоумышленника по выбору ключей по степени связанности.
Другая атака была описана в блоге Брюса Шнайера [3] 30 июля 2009 года и выпущена в виде препринта [22] 3 августа 2009 года. Эта новая атака, предпринятая Алексом Бирюковым, Орром Данкельманом , Натаном Келлером, Дмитрием Ховратовичем и Ади Шамиром , направлена против AES-256, который использует только два связанных ключа и 2,39 времени для восстановления полного 256-битного ключа 9-раундовой версии, или 2,45 времени для 10-раундовой версии с более сильным типом связанной атаки на подключ, или 2,70 времени для 11-раундовой версии. 256-битный AES использует 14 раундов, поэтому эти атаки неэффективны против полного AES.
Практичность этих атак с более сильными связанными ключами подвергалась критике, [23] например, в статье об атаках с выбранными ключами-связями-в-середине на AES-128, написанной Винсентом Рейменом в 2010 году. [24]
В ноябре 2009 года была выпущена первая атака с известным ключом, направленная против сокращенной версии AES-128 с 8 раундами. [25] Эта атака с известным ключом, направленная против перестановок, подобных AES, представляет собой усовершенствование атаки rebound или start-from-the-middle, направленной против перестановок, подобных AES, которая рассматривает два последовательных раунда перестановки как применение так называемого Super-S-box. Она работает с версией AES-128 с 8 раундами, с временной сложностью 2 48 и сложностью памяти 2 32 . 128-битный AES использует 10 раундов, поэтому эта атака неэффективна против полного AES-128.
Первые атаки с восстановлением ключа на полный AES были проведены Андреем Богдановым, Дмитрием Ховратовичем и Кристианом Рехбергером и опубликованы в 2011 году. [26] Атака представляет собой атаку biclique и быстрее, чем brute force примерно в четыре раза. Для восстановления ключа AES-128 требуется 2 126,2 операций. Для AES-192 и AES-256 требуется 2 190,2 и 2 254,6 операций соответственно. Этот результат был дополнительно улучшен до 2 126,0 для AES-128, 2 189,9 для AES-192 и 2 254,3 для AES-256 Бяошуай Тао и Хунцзюнь У в статье 2015 года [27] , что является лучшими на данный момент результатами в атаке с восстановлением ключа против AES.
Это очень небольшой выигрыш, так как 126-битный ключ (вместо 128 бит) все еще потребуют миллиарды лет для подбора на текущем и прогнозируемом оборудовании. Кроме того, авторы вычисляют лучшую атаку с использованием своей техники на AES с 128-битным ключом, требующую хранения 2 88 бит данных. Это составляет около 38 триллионов терабайт данных, что больше, чем все данные, хранящиеся на всех компьютерах на планете в 2016 году. [28] Позже в статье 2015 года пространственная сложность была улучшена до 2 56 бит, [27] что составляет 9007 терабайт (при этом временная сложность все еще сохранялась примерно 2 126 ).
Согласно документам Сноудена , АНБ проводит исследование на тему, может ли криптографическая атака, основанная на статистике тау, помочь взломать AES. [29]
В настоящее время не существует известной практической атаки, которая позволила бы кому-либо без знания ключа прочитать данные, зашифрованные AES, при правильной реализации. [ необходима цитата ]
Атаки по побочным каналам
Атаки по сторонним каналам не атакуют шифр как черный ящик , и, таким образом, не связаны с безопасностью шифра, как она определена в классическом контексте, но важны на практике. Они атакуют реализации шифра на аппаратных или программных системах, которые непреднамеренно допускают утечку данных. Известно несколько таких атак на различные реализации AES.
В апреле 2005 года D. J. Bernstein объявил об атаке с использованием кэша, которую он использовал для взлома пользовательского сервера, использовавшего шифрование AES OpenSSL . [30] Для атаки потребовалось более 200 миллионов выбранных открытых текстов. [31] Пользовательский сервер был разработан для выдачи как можно большего количества информации о времени (сервер сообщает количество машинных циклов, затраченных на операцию шифрования). Однако, как указал Bernstein, «снижение точности временных меток сервера или их исключение из ответов сервера не останавливает атаку: клиент просто использует тайминги кругового обхода на основе своих локальных часов и компенсирует возросший шум путем усреднения по большему количеству выборок». [30]
В октябре 2005 года Даг Арне Освик, Ади Шамир и Эран Тромер представили документ, демонстрирующий несколько атак с использованием кэш-тайминга против реализаций AES, обнаруженных в OpenSSL и dm-cryptфункции шифрования разделов Linux. [32] Одна атака позволила получить весь ключ AES всего за 800 операций, запускающих шифрование, всего за 65 миллисекунд. Эта атака требует, чтобы злоумышленник мог запускать программы на той же системе или платформе, которая выполняет AES.
В декабре 2009 года была опубликована атака на некоторые аппаратные реализации, которая использовала дифференциальный анализ неисправностей и позволяла восстановить ключ со сложностью 2 32 . [33]
В ноябре 2010 года Эндре Бангертер, Дэвид Гуллаш и Стефан Кренн опубликовали статью, в которой описали практический подход к восстановлению секретных ключей из AES-128 «почти в реальном времени» без необходимости в зашифрованном тексте или открытом тексте. Этот подход также работает в реализациях AES-128, использующих таблицы сжатия, такие как OpenSSL. [34] Как и некоторые более ранние атаки, эта требует возможности запустить непривилегированный код в системе, выполняющей шифрование AES, что может быть достигнуто путем заражения вредоносным ПО гораздо проще, чем захват учетной записи root. [35]
В марте 2016 года С. Ашоккумар, Рави Пракаш Гири и Бернард Менезес представили атаку по побочному каналу на реализации AES, которая позволяет восстановить полный 128-битный ключ AES всего за 6–7 блоков открытого текста/шифртекста, что является существенным улучшением по сравнению с предыдущими работами, которые требовали от 100 до миллиона шифрований. [36] Предлагаемая атака требует стандартных привилегий пользователя и алгоритмов извлечения ключей, работающих менее чем за минуту.
Многие современные процессоры имеют встроенные аппаратные инструкции для AES , которые защищают от атак по побочным каналам, связанных с синхронизацией. [37] [38]
Квантовые атаки
AES-256 считается квантово- устойчивым, так как имеет квантовую устойчивость, аналогичную устойчивости AES-128 к традиционным, неквантовым, атакам при 128 битах безопасности . AES-192 и AES-128 не считаются квантово-устойчивыми из-за меньших размеров ключей. AES-192 имеет стойкость 96 бит против квантовых атак, а AES-128 имеет стойкость 64 бита против квантовых атак, что делает их оба небезопасными. [39] [40]
Проверка NIST/CSEC
Программа проверки криптографических модулей (CMVP) совместно управляется Отделом компьютерной безопасности Национального института стандартов и технологий (NIST) правительства США и Управлением безопасности коммуникаций (CSE) правительства Канады. Использование криптографических модулей, проверенных в соответствии с NIST FIPS 140-2, требуется правительством США для шифрования всех данных, имеющих классификацию « Конфиденциальные, но неклассифицированные» (SBU) или выше. Из NSTISSP #11, Национальная политика, регулирующая получение гарантии информации: «Продукты шифрования для защиты секретной информации будут сертифицированы АНБ, а продукты шифрования, предназначенные для защиты конфиденциальной информации, будут сертифицированы в соответствии с NIST FIPS 140-2». [41]
Правительство Канады также рекомендует использовать криптографические модули, проверенные на соответствие стандарту FIPS 140, в несекретных приложениях своих ведомств.
Хотя публикация NIST 197 («FIPS 197») является уникальным документом, который охватывает алгоритм AES, поставщики обычно обращаются к CMVP в соответствии с FIPS 140 и просят провести одновременную проверку нескольких алгоритмов (например, Triple DES или SHA1 ). Поэтому редко можно найти криптографические модули, которые однозначно проверены по FIPS 197, и сам NIST обычно не тратит время на то, чтобы отдельно перечислить проверенные по FIPS 197 модули на своем общедоступном веб-сайте. Вместо этого проверка по FIPS 197 обычно просто указывается как нотация «Одобрено FIPS: AES» (с определенным номером сертификата FIPS 197) в текущем списке проверенных по FIPS 140 криптографических модулей.
Программа проверки криптографических алгоритмов (CAVP) [42] позволяет проводить независимую проверку правильности реализации алгоритма AES. Успешная проверка приводит к включению в список на странице проверок NIST. [43] Это тестирование является предварительным условием для проверки модуля FIPS 140-2. Однако успешная проверка CAVP никоим образом не означает, что криптографический модуль, реализующий алгоритм, является безопасным. Криптографический модуль, не прошедший проверку FIPS 140-2 или не получивший специального одобрения NSA, не считается безопасным правительством США и не может использоваться для защиты правительственных данных. [41]
Валидация FIPS 140-2 является сложной задачей как с технической, так и с финансовой точки зрения. [44] Существует стандартизированный набор тестов, а также элемент обзора исходного кода, который должен быть пройден в течение нескольких недель. Стоимость проведения этих тестов в одобренной лаборатории может быть значительной (например, значительно более 30 000 долларов США) [44] и не включает время, необходимое для написания, тестирования, документирования и подготовки модуля к валидации. После валидации модули должны быть повторно представлены и повторно оценены, если они каким-либо образом изменены. Это может варьироваться от простых обновлений документов, если функциональность безопасности не изменилась, до более существенного набора повторных тестов, если функциональность безопасности была затронута изменением.
Тестовые векторы
Тестовые векторы — это набор известных шифров для заданного ввода и ключа. NIST распространяет ссылку на тестовые векторы AES как AES Known Answer Test (KAT) Vectors. [примечание 7]
Производительность
Высокая скорость и низкие требования к оперативной памяти были одними из критериев процесса выбора AES. В качестве выбранного алгоритма AES хорошо показал себя на широком спектре оборудования, от 8-битных смарт-карт до высокопроизводительных компьютеров.
На Pentium Pro шифрование AES требует 18 тактов на байт (cpb), [45] что эквивалентно пропускной способности около 11 МБ/с для процессора с тактовой частотой 200 МГц.
На процессорах Intel Core и AMD Ryzen , поддерживающих расширения набора инструкций AES-NI , пропускная способность может составлять несколько ГиБ/с. [46] На процессоре Intel Westmere шифрование AES с использованием AES-NI занимает около 1,3 cpb для AES-128 и 1,8 cpb для AES-256. [47]
Реализации
Смотрите также
- Режимы работы AES
- Шифрование диска
- Whirlpool – хэш-функция, созданная Винсентом Рейменом и Пауло СЛМ Баррето
- Список бесплатных и открытых пакетов программного обеспечения
Примечания
- ^ Алгоритм Rijndael поддерживает ключи длиной 128, 160, 192, 224 и 256 бит, но в стандарте AES указаны только ключи длиной 128, 192 и 256 бит.
- ^ Алгоритм Rijndael поддерживает размеры блока 128, 160, 192, 224 и 256 бит для каждого размера ключа, но в стандарте AES указан только размер блока в 128 бит.
- ^ Более подробную информацию см . в разделе «Процесс расширенного стандарта шифрования» .
- ^ См. раздел «Безопасность AES» ниже.
- ^ Варианты Rijndael с большими блоками используют массив с дополнительными столбцами, но всегда четырьмя строками.
- ^ Варианты Rijndael с большим размером блока имеют немного отличающиеся смещения. Для блоков размером 128 бит и 192 бита шаблон сдвига тот же. Строка сдвигается влево по кругу на байт. Для 256-битного блока первая строка остается неизменной, а сдвиг для второй, третьей и четвертой строк составляет 1 байт, 3 байта и 4 байта соответственно — это изменение применяется только к шифру Rijndael при использовании с 256-битным блоком, поскольку AES не использует 256-битные блоки.
- ^ Векторы теста известных ответов AES (KAT) доступны в формате Zip на сайте NIST здесь. Архивировано 23 октября 2009 г. на Wayback Machine.
Ссылки
- ^ "Biclique Cryptanalysis of the Full AES" (PDF) . Архивировано из оригинала (PDF) 6 марта 2016 г. . Получено 1 мая 2019 г. .
- ^ ab Алекс Бирюков и Дмитрий Ховратович, Related-key Cryptanalysis of the Full AES-192 and AES-256 , "Related-key Cryptanalysis of the Full AES-192 and AES-256". Таблица 1. Архивировано из оригинала 2009-09-28 . Получено 2010-02-16 .
- ^ ab Bruce Schneier (2009-07-30). "Еще одна новая атака AES". Schneier on Security, блог, посвященный безопасности и технологиям безопасности . Архивировано из оригинала 2009-10-05 . Получено 2010-03-11 .
- ^ Алекс Бирюков; Орр Данкельман; Натан Келлер; Дмитрий Ховратович; Ади Шамир (2009-08-19). "Атаки по восстановлению ключей практической сложности на варианты AES с количеством раундов до 10". Архивировано из оригинала 28 января 2010 года . Получено 2010-03-11 .
- ^ ab Daemen, Joan; Rijmen, Vincent (9 марта 2003 г.). "Предложение AES: Rijndael" (PDF) . Национальный институт стандартов и технологий. стр. 1. Архивировано (PDF) из оригинала 5 марта 2013 г. . Получено 21 февраля 2013 г. .
- ^ abc "Annovating the ADVANCED ENCRYPTION STANDARD (AES)" (PDF) . Федеральные стандарты обработки информации Публикация 197 . Национальный институт стандартов и технологий США (NIST). 26 ноября 2001 г. Архивировано (PDF) из оригинала 23 августа 2024 г. . Получено 26 августа 2024 г. .
- ^ Джоан Даемен и Винсент Реймен (3 сентября 1999 г.). "Предложение AES: Rijndael" (PDF) . Архивировано из оригинала (PDF) 3 февраля 2007 г.
- ↑ Джон Шварц (3 октября 2000 г.). «США выбирают новый метод шифрования». New York Times . Архивировано из оригинала 28 марта 2017 г.
- ^ Вестлунд, Гарольд Б. (2002). "NIST сообщает об измеримом успехе Advanced Encryption Standard". Журнал исследований Национального института стандартов и технологий . Архивировано из оригинала 2007-11-03.
- ^ "ISO/IEC 18033-3: Информационные технологии — Методы обеспечения безопасности — Алгоритмы шифрования — Часть 3: Блочные шифры". Архивировано из оригинала 2013-12-03.
- ^ Брюс Шнайер; Джон Келси; Дуг Уайтинг; Дэвид Вагнер; Крис Холл; Нильс Фергюсон; Тадаёши Коно; и др. (май 2000 г.). «Заключительные комментарии команды Twofish по выбору AES» (PDF) . Архивировано (PDF) из оригинала 2010-01-02.
- ^ Бертони, Гвидо; Бревельери, Лука; Фрагнето, Паскуалина; МакКетти, Марко; Марчезин, Стефано (2003). "Эффективная программная реализация AES на 32-битных платформах". Криптографическое оборудование и встраиваемые системы - CHES 2002. Конспект лекций по информатике. Том 2523. С. 159–171 . doi :10.1007/3-540-36400-5_13. ISBN 978-3-540-00409-7.
- ^ "byte-oriented-aes – общедоступная байт-ориентированная реализация AES на языке C – Google Project Hosting". Архивировано из оригинала 2013-07-20 . Получено 2012-12-23 .
- ^ Линн Хэтэуэй (июнь 2003 г.). «Национальная политика использования усовершенствованного стандарта шифрования (AES) для защиты систем национальной безопасности и информации о национальной безопасности» (PDF) . Архивировано (PDF) из оригинала 2010-11-06 . Получено 2011-02-15 .
- ^ Джон Келси , Стефан Лакс , Брюс Шнайер , Майк Стэй, Дэвид Вагнер и Дуг Уайтинг, Улучшенный криптоанализ Rijndael , Быстрое программное шифрование , 2000, стр. 213–230 «Академический: Улучшенный криптоанализ Rijndael — Шнайер о безопасности». Архивировано из оригинала 23.02.2007 . Получено 06.03.2007 .
- ↑ Ou, George (30 апреля 2006 г.). «Действительно ли шифрование можно взломать?». Ziff-Davis. Архивировано из оригинала 8 августа 2010 г. Получено 7 августа 2010 г.
- ^ "Шон Мерфи". Лондонский университет. Архивировано из оригинала 2009-01-31 . Получено 2008-11-02 .
- ^ Брюс Шнайер. "AES News, Crypto-Gram Newsletter, 15 сентября 2002 г.". Архивировано из оригинала 7 июля 2007 г. Получено 27 июля 2007 г.
- ^ Нильс Фергюсон ; Ричард Шрёппель ; Дуг Уайтинг (2001). "Простое алгебраическое представление Rijndael". Труды избранных областей криптографии, 2001, Lecture Notes in Computer Science . Springer-Verlag . стр. 103–111 . CiteSeerX 10.1.1.28.4921 . Архивировано из оригинала (PDF/ PostScript ) 4 ноября 2006 года . Получено 06.10.2006 .
- ↑ Брюс Шнайер, AES Анонсировано Архивировано 01.02.2009 в Wayback Machine , 15 октября 2000 г.
- ^ Николич, Ивица (2009). «Distinguisher and Related-Key Attack on the Full AES-256». Достижения в криптологии - CRYPTO 2009. Конспект лекций по информатике. Том 5677. Springer Berlin / Heidelberg. С. 231– 249. doi :10.1007/978-3-642-03356-8_14. ISBN 978-3-642-03355-1.
- ^ Алекс Бирюков; Орр Данкельман; Натан Келлер; Дмитрий Ховратович; Ади Шамир (2009-08-19). "Атаки по восстановлению ключей практической сложности на варианты AES с количеством раундов до 10". Архивировано из оригинала 28 января 2010 года . Получено 2010-03-11 .
- ^ Агрен, Мартин (2012). О некоторых симметричных облегченных криптографических схемах . Диссертация, Лундский университет. С. 38–39 .
- ^ Винсент Раймен (2010). "Практическая атака на AES-128 с использованием отношений выбранного текста" (PDF) . Архив IACR Cryptology ePrint . Архивировано (PDF) из оригинала 2010-07-02.
- ^ Анри Жильбер; Томас Пейрен (2009-11-09). "Super-Sbox Cryptanalysis: Improved Attacks for AES-like permutations". Архив IACR Cryptology ePrint . Архивировано из оригинала 2010-06-04 . Получено 2010-03-11 .
- ^ Богданов, Андрей; Ховратович, Дмитрий; Рехбергер, Кристиан (2011). «Biclique Cryptanalysis of the Full AES». В Lee, Dong Hoon; Wang, Xiaoyun (ред.). Advances in Cryptology – ASIACRYPT 2011. Lecture Notes in Computer Science. Vol. 7073. pp. 344– 371. doi :10.1007/978-3-642-25385-0_19. ISBN 978-3-642-25385-0.
- ^ ab Tao, Biaoshuai; Wu, Hongjun (2015). «Улучшение Biclique Cryptanalysis of AES». В Foo, Ernest; Stebila, Douglas (ред.). Информационная безопасность и конфиденциальность . Конспект лекций по информатике. Том 9144. С. 39–56 . doi :10.1007/978-3-319-19962-7_3. ISBN 978-3-319-19962-7.
- ^ Джеффри Голдберг (2011-08-18). «Шифрование AES не взломано». Архивировано из оригинала 8 января 2015 года . Получено 30 декабря 2014 года .
- ^ "Prying Eyes: Inside the NSA's War on Internet Security". Spiegel Online . Гамбург, Германия. 28 декабря 2014 г. Архивировано из оригинала 24 января 2015 г. Получено 4 сентября 2015 г.
- ^ ab "Индекс официальных научных статей". Cr.yp.to. Архивировано из оригинала 2008-09-17 . Получено 2008-11-02 .
- ^ Брюс Шнайер. "AES Timing Attack". Архивировано из оригинала 12 февраля 2007 года . Получено 2007-03-17 .
- ^ Даг Арне Освик; Ади Шамир; Эран Тромер (2005-11-20). "Атаки на кэш и контрмеры: случай AES" (PDF) . Трек криптографа на конференции RSA 2006 . doi :10.1007/11605805_1. Архивировано (PDF) из оригинала 2006-06-19 . Получено 2008-11-02 .
- ^ Диман Саха; Дебдип Мукхопадьяй; Дипанвита Рой Чоудхури . «Атака по диагональной ошибке на расширенный стандарт шифрования» (PDF) . Архив электронной печати криптологии IACR . Архивировано (PDF) из оригинала 22 декабря 2009 г. Проверено 8 декабря 2009 г.
- ^ Эндре Бангертер; Дэвид Гуллаш и Стефан Кренн (2010). «Игры в кэш – внедрение атак на кэш на основе доступа к AES на практике» (PDF) . Архив IACR Cryptology ePrint . Архивировано (PDF) из оригинала 14.12.2010.
- ^ "Взлом AES-128 в реальном времени, шифртекст не требуется". Hacker News. Архивировано из оригинала 2011-10-03 . Получено 2012-12-23 .
- ^ Ashokkumar, C.; Giri, Ravi Prakash; Menezes, Bernard. Высокоэффективные алгоритмы извлечения ключей AES при атаках на доступ к кэшу . Европейский симпозиум IEEE по безопасности и конфиденциальности 2016 г. (EuroS&P). Саарбрюккен, Германия. стр. 261–275 . doi :10.1109/EuroSP.2016.29.
- ^ Mowery, Keaton; Keelveedhi, Sriram; Shacham, Hovav (19 октября 2012 г.). Возможны ли атаки по времени кэша AES x86? (PDF) . CCS'12: конференция ACM по компьютерной и коммуникационной безопасности. Роли, Северная Каролина, США. стр. 19–24 . doi :10.1145/2381913.2381917. Архивировано из оригинала (PDF) 2017-08-09.
- ^ "Securing the Enterprise with Intel AES-NI" (PDF) . Корпорация Intel . Архивировано (PDF) из оригинала 2013-03-31 . Получено 2017-07-26 .
- ^ Боннетэн, Ксавье; Найя-Пласенсия, Мария; Шроттенлоэр, Андре (11 июня 2019 г.). «Квантовый анализ безопасности AES». Транзакции IACR по симметричной криптологии . 2019 (2): 55–93 . doi : 10.13154/tosc.v2019.i2.55-93 .
- ^ О'Ши, Дэн (26 апреля 2022 г.). «AES-256 присоединяется к квантовому сопротивлению». Fierce Electronics . Получено 26 сентября 2023 г. .
- ^ ab "NSTISSP № 11, Пересмотренный информационный бюллетень, Национальная политика обеспечения информации" (PDF) . Архивировано из оригинала (PDF) 2012-04-21 . Получено 2012-05-29 .
- ^ "NIST.gov – Computer Security Division – Computer Security Resource Center". Csrc.nist.gov. Архивировано из оригинала 2013-01-02 . Получено 2012-12-23 .
- ^ "Проверенные криптографические модули FIPS 140-1 и FIPS 140-2". Архивировано из оригинала 2014-12-26 . Получено 2014-06-26 .
- ^ ab OpenSSL, openssl@openssl.org. "Заметки OpenSSL о сертификации FIPS". Openssl.org. Архивировано из оригинала 2013-01-02 . Получено 2012-12-23 .
- ^ Шнайер, Брюс; Келси, Джон; Уайтинг, Дуг; Вагнер, Дэвид; Холл, Крис; Фергюсон, Нильс (1999-02-01). "Сравнение производительности заявок AES" (PDF) . Архивировано (PDF) из оригинала 2011-06-22 . Получено 2010-12-28 .
- ^ «Обзор AMD Ryzen 7 1700X».
- ^ «Новый набор инструкций Intel ® Advanced Encryption Standard (AES)» (PDF) . Май 2010 г.
- Куртуа, Николя; Пиепшик, Йозеф (2003). «Криптоанализ блочных шифров с переопределенными системами уравнений». В Чжэн, Юйлян (ред.). Достижения в криптологии – ASIACRYPT 2002: 8-я международная конференция по теории и применению криптологии и информационной безопасности, Квинстаун, Новая Зеландия, 1–5 декабря 2002 г., Труды . Springer. стр. 268–287 . ISBN 978-3-540-36178-7.
- Дэмен, Джоан; Реймен, Винсент (2002). Дизайн Rijndael: AES – расширенный стандарт шифрования. Спрингер. ISBN 978-3-540-42580-9.
- Paar, Christof; Pelzl, Jan (2009). Understanding Cryptography: A Textbook for Students and Practitioners. Springer. С. 87–122 . ISBN 978-3-642-04101-3.альтернативная ссылка (сопутствующий веб-сайт содержит онлайн-лекции по AES)
Внешние ссылки
- «256-битный ключ – 128-битный блок – AES». Криптография – 256-битные шифры: Исходный код и заявки на международные конкурсы криптографических разработок . EmbeddedSW.
- "Advanced Encryption Standard (AES)" (PDF) . Федеральные стандарты обработки информации . 26 ноября 2001 г. doi : 10.6028/NIST.FIPS.197 . 197.
- Архивная информация об алгоритме AES – (старая, не поддерживается)
- "Часть 3: Блочные шифры" (PDF) . Информационные технологии – Методы безопасности – Алгоритмы шифрования (2-е изд.). ISO. 2010-12-15. ISO/IEC 18033-3:2010(E). Архивировано (PDF) из оригинала 2022-10-09.
- Анимация Rijndael – AES подробно объяснена и анимирована с использованием Flash (Энрике Забала / Университет ORT / Монтевидео / Уругвай). Эта анимация (на английском, испанском и немецком языках) также является частью CrypTool 1 (меню Indiv. Procedures → Visualization of Algorithms → AES).
- HTML5-анимация Rijndael – та же анимация, что и выше, выполненная в HTML5.












![{\displaystyle \operatorname {GF} (2)[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6334bd0b6ddc3a60f9d7590f71c74e11f780b80f)

